题目内容
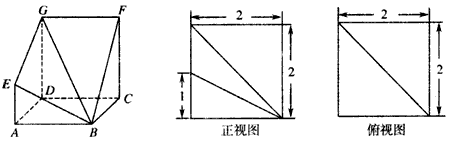
如图,多面体ABCDS中,面ABCD为矩形,![]()
![]()
(I)求多面体ABCDS的体积;
(II)求AD与SB所成角的余弦值。
(III)求二面角A—SB—D的余弦值。

(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
解析:
(I)多面体ABCDS的体积即四棱锥S—ABCD的体积。
所以![]() …………4分
…………4分
(II)由题可知DA、DA、DC两两互相垂直,
![]() 如图建立空间直角坐标系
如图建立空间直角坐标系

![]()
![]()

![]() AD与SB所成的角的余弦为
AD与SB所成的角的余弦为![]() …………9分
…………9分
(III)![]() 设面SBD的一个法向量为
设面SBD的一个法向量为![]()

又![]()
![]() 设面SAB的一个法向量为
设面SAB的一个法向量为![]()
 …………11分
…………11分
![]() ,
,
所以所求的二面角的余弦为![]() …………14分
…………14分
解法二:(I)同解法一
(II)![]() 矩形ABCD,
矩形ABCD,
![]() AD
AD![]() BC,即BC=a,
BC,即BC=a,
![]() 要求AD与SB所成的角,即求BC与SB所成的角。…………6分
要求AD与SB所成的角,即求BC与SB所成的角。…………6分
在![]() 中,由(1)知
中,由(1)知![]() 面ABCD。
面ABCD。
![]()
![]() CD是CS在面ABCD内的射影,且
CD是CS在面ABCD内的射影,且![]()
![]()
![]()

![]() BC与SB所成的角的余弦为
BC与SB所成的角的余弦为![]()
从而SB与AD的成的角的余弦为![]() …………9分
…………9分
(III)![]()
![]() 面ABCD。
面ABCD。
![]() BD为面SDB与面ABCD的交线。
BD为面SDB与面ABCD的交线。
![]()
![]() SDB
SDB
![]() 于F,连接EF
于F,连接EF
从而得:![]()
![]() 为二面角A—SB—D的平面角…………11分
为二面角A—SB—D的平面角…………11分
在矩形ABCD中,对角线![]()
![]() 中,
中,![]()
由(2)知在![]()
而![]()
![]()
![]() 为等腰直角三角形且
为等腰直角三角形且![]()
![]()
 ,
,
所以所求的二面角的余弦为![]() …………14分
…………14分



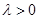 使得
使得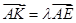 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为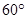 ,求
,求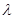 的值。
的值。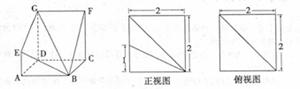
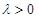 使得
使得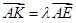 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为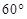 ,求
,求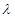 的值。
的值。
 使得
使得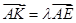 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为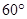 ,求
,求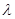 的值。
的值。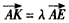 ,KF与平面ABG所成角为30°,求λ的值。
,KF与平面ABG所成角为30°,求λ的值。