Question

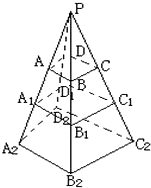
如图，已知正四棱锥V-ABCD中，AC与BD交于点M，VM是棱锥的高，若AC=8cm，VC=5cm，求正四棱锥V-ABCD的体积．

Answer 1

∵正四棱锥V-ABCD中，底面ABCD是正方形，且对角线AC=8cm，VM是棱锥的高
∴BD=8cm，且AC⊥BD
∴S_ABCD=4×

1

2

×4×4=32（cm²）
∵VM是棱锥的高，且VC=5cm
∴Rt△VMC中，VM=

VC2-CM2

=3（cm）
∴正四棱锥V-ABCD的体积为V=

1

3

×S_ABCD×VM=

1

3

×32×3=32（cm³）