Question

已知椭圆=1(a＞b＞0),A、B是椭圆上的两点,线段AB的垂直平分线与x轴相交于点P(x₀,0).证明－＜x₀＜.

Answer 1

证法一:设A(x₁,y₁)、B(x₂,y₂),则线段AB的垂直平分线方程为

y－=－(x－).

令y=0,得x=x₀=+=.                                      (*)

又=1,                                                                                                       ①

=1,                                                                                                         ②

②－①得=－,代入(*)得

x₀=·.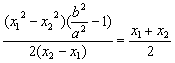

由－a≤x₁≤a,－a≤x₂≤a,x₁≠x₂,

知－a＜＜a.又＞0,

∴－＜·＜,

即－＜x₀＜.

证法二:设A、B的坐标分别为(x₁,y₁)和(x₂,y₂),线段AB的垂直平分线与x轴相交,故AB不平行于y轴,即x₁≠x₂.又交点为P(x₀,0),

故|PA|=|PB|,即(x₁－x₀)²+y₁²=(x₂－x₀)²+y₂².                                                                ①

∵A、B在椭圆上,

∴=1,  =1,代入①得

2(x₂－x₁)x₀=(x₂²－x₁²)·,

即x₀=· (下同证法一).