题目内容
随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为ξ.(1)求ξ的分布列;
(2)求1件产品的平均利润(即ξ的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
解:(1)ξ的可能取值为6,2,1,-2,
P(ξ=6)=![]() =0.63,
=0.63,
P(ξ=2)=![]() =0.25,
=0.25,
P(ξ=1)=![]() =0.1,
=0.1,
P(ξ=-2)=![]() =0.02,
=0.02,
∴ξ的分布列为
ξ | 6 | 2 | 1 | -2 |
P | 0.63 | 0.25 | 0.1 | 0.02 |
(2)Eξ=0.63×6+0.25×2+0.1×1+0.02×(-2)=4.34.
答:一件产品的平均利润为4.34万元.
(3)设三等品率为x,依题意,有0.7×6+0.01×(-2)+x×1+(0.29-x)×2≥4.73.
∴x≤0.03.
答:三等品率最多为3%.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
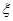 .
.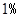 ,一等品率提高为
,一等品率提高为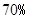 .如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?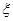 。
。