题目内容
(2004•朝阳区一模)已知F1、F2是椭圆
+
=1的左、右焦点,P为椭圆上一个点,且|PF1|:|PF2|=1:2,则tan∠F1PF2=
,PF2的斜率为
| x2 |
| 9 |
| y2 |
| 5 |
| 15 |
| 15 |
-
| ||
| 7 |
-
.
| ||
| 7 |
分析:利用椭圆的定义,结合三角函数的定义可求∠F1PF2的正切值,求出tan∠PF2F1=
=
,可得PF2的斜率.
| ||||
|
| ||
| 7 |
解答:解:由题意,|PF1|+|PF2|=6,|F1F2|=4,
∵|PF1|:|PF2|=1:2,∴|PF1|2,|PF2|=4,
∴△PF1F2为等腰三角形,底边上的高为
=
∴tan∠F1PF2=
由等面积可得,P到x轴的距离为
∵
=
∴tan∠PF2F1=
=
∴PF2的斜率为-
故答案为:
,-
∵|PF1|:|PF2|=1:2,∴|PF1|2,|PF2|=4,
∴△PF1F2为等腰三角形,底边上的高为
| 16-1 |
| 15 |
∴tan∠F1PF2=
| 15 |
由等面积可得,P到x轴的距离为
| ||
| 2 |
∵
42-(
|
| 7 |
| 2 |
∴tan∠PF2F1=
| ||||
|
| ||
| 7 |
∴PF2的斜率为-
| ||
| 7 |
故答案为:
| 15 |
| ||
| 7 |
点评:本题考查椭圆的定义,考查三角函数的定义,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
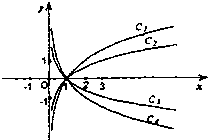 (2004•朝阳区一模)已知图中曲线C1、C2、C3、C4是函数logax的图象,则曲线C1、C2、C3、C4对应的a的值依次为( )
(2004•朝阳区一模)已知图中曲线C1、C2、C3、C4是函数logax的图象,则曲线C1、C2、C3、C4对应的a的值依次为( )