Question

曲线f(x)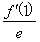＝ ex－f(0)x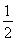＋ x2在点(1，f(1))处的切线方程为________．

 

Answer 1

y＝ex－

【解析】由已知得f(0)＝，

∴f(x)＝ ex－ x＋ x2，

∴f′(x)＝ ex－＋x，

∴f′(1)＝ e－＋1，即f′(1)＝e，

从而f(x)＝ex－x＋ x2，f′(x)＝ex－1＋x，

∴f(1)＝e－，f′(1)＝e，

故切线方程为y－＝e(x－1)，即y＝ex－.