题目内容
定义函数y=f（x），x∈D．若存在常数c，对任意x1∈D，存在唯一的x2∈D，使得
，则称函数f（x）在D上的算术平均数为c．已知f（x）=lnx，x∈[2，8]，则f（x）=lnx在[2，8]上的算术平均数为
- A.ln2
- B.ln4
- C.ln5
- D.ln8
B
分析：根据定义，令x1•x2=2×8=16当x1∈[2，8]时，选定
可得：
解答：根据定义，函数y=f（x），x∈D，若存在常数C，对任意的x1∈D，存在唯一的x2∈D，使得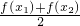
=C，则称函数f（x）在D上的均值为C．
令x1•x2=2×8=16
当x1∈[2，8]时，选定
可得：
故选B．
点评：这种题型可称为创新题型或叫即时定义题型．关键是要读懂题意．充分利用即时定义来答题．
分析：根据定义，令x1•x2=2×8=16当x1∈[2，8]时，选定
可得：解答：根据定义，函数y=f（x），x∈D，若存在常数C，对任意的x1∈D，存在唯一的x2∈D，使得
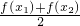=C，则称函数f（x）在D上的均值为C．令x1•x2=2×8=16
当x1∈[2，8]时，选定
可得：
故选B．
点评：这种题型可称为创新题型或叫即时定义题型．关键是要读懂题意．充分利用即时定义来答题．
练习册系列答案
相关题目