题目内容
设函数f(x)=m·n,其中m=(2cosx,1),n=(cosx,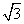 sinx),x∈R。
sinx),x∈R。
(1)求f(x)的最小正周期与单调减区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,且f(A)=2
①求A;
②若b=1,△ABC的面积为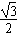 ,求
,求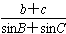 的值。
的值。
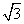 sinx),x∈R。
sinx),x∈R。(1)求f(x)的最小正周期与单调减区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,且f(A)=2
①求A;
②若b=1,△ABC的面积为
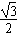 ,求
,求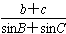 的值。
的值。解:f(x)=m·n=2cos2x+ sin2x=1+cos2x+
sin2x=1+cos2x+ sin2x=2sin(2x+
sin2x=2sin(2x+ )+1
)+1
(1)函数f(x)的最小正周期T=π
令
∴
∴ (k∈Z)
(k∈Z)
∴f(x)的单调减区间为 ;
;
(2)①
∴ =
=
∵
∴
∴ 。
。
②
∴c=2
在△ABC中,由余弦定理得,

∴
由正弦定理得,
∴ ,
,
∴ 2。
2。
 sin2x=1+cos2x+
sin2x=1+cos2x+ sin2x=2sin(2x+
sin2x=2sin(2x+ )+1
)+1(1)函数f(x)的最小正周期T=π
令

∴

∴
 (k∈Z)
(k∈Z)∴f(x)的单调减区间为
 ;
;(2)①

∴
 =
=
∵

∴

∴
 。
。②

∴c=2
在△ABC中,由余弦定理得,

∴

由正弦定理得,

∴
 ,
,
∴
 2。
2。
练习册系列答案
相关题目