题目内容

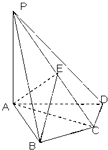
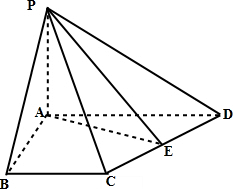
如图，点P为矩形ABCD所在平面外一点，PA⊥平面ABCD，E，F分别为线段PB，PC的中点，且AD=4，PA=AB=2
（1）求直线EC和面PAD所成的角
（2）求点P到平面AFD的距离．
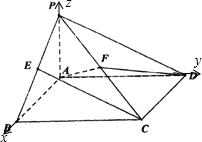
（1）分别以AB，AD，AP为x，y，z轴，建立空间直角坐标系，
则A（0，0，0），B（2，0，0），C（2，4，0），D（0，4，0），P（0，0，2）
∴E（1，0，1），F（1，2，1），
EC
=(1，4，-1)
∵AB⊥平面PAD
∴平面PAD的法向量为
AB
=（2，0，0）
设直线EC与平面PAD所成的角为α，则sinα=
EC
•
AB
|
EC
||
AB
|
=
2
6

∴直线EC与平面PAD所成的角为arcsin
2
6
；
（2）由（1）可知
AF
=(1，2，1)，
AD
=(0，4，0)
设平面AFD的法向量为
n
=（x，y，z），点P到平面AFD的距离为d
由
AF
•
n
=0
AD
•
n
=0
，可得
x+2y+z=0
4y=0
，∴取
n
=（1，0，-1）
∵
AP
=(0，0，2)
∴d=
|
AP
•
n
|
|
n
|
=
2
．
练习册系列答案
相关题目
如图所示，已知S是正三角形ABC所在平面外的一点，且SA=SB=SC，SG为△SAB上的高，D、E、F分别是AC、BC、SC的中点，试判断SG与平面DEF的位置关系，并给予证明.
若平面α与β的法向量分别是
a
=(2，4，-3)，
b
=(-1，2，2)，则平面α与β的位置关系是（　　）
A．平行B．垂直
C．相交但不垂直D．无法确定
如图，三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC，∠ACB=90°，E是棱CC1上动点，F是AB中点，AC=1，BC=2，AA1=4．
（1）当E是棱CC1中点时，求证：CF∥平面AEB1；
（2）在棱CC1上是否存在点E，使得二面角A-EB1-B的余弦值是
2
17
17
，若存在，求CE的长，若不存在，请说明理由．
底面ABCD为矩形的四棱锥P-ABCD中，AB=
3
，BC=1，PA=2，侧棱PA⊥底面ABCD，E为PD的中点
（Ⅰ）求直线AC与PB所成角的余弦值；
（Ⅱ）在侧面PAB内找一点N，使NE⊥面PAC，并求出点N到AB和AP的距离．
在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．
（1）证明：CD⊥AE；
（2）证明：PD⊥平面ABE；
（3）求二面角B-PC-D的余弦值．
如图，在三棱锥P-ABC中，PA⊥底面ABC，∠ACB=90°，AE⊥PB于E，AF⊥PC于F，若PA=AB=2，∠BPC=θ，则当△AEF的面积最大时，tanθ的值为（　　）
A．2B．
1
2
C．
2
D．
2
2
如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AB=4，BC=3，AD=5，∠DAB=∠ABC=90°，E是CD的中点．
（Ⅰ）证明：CD⊥平面PAE；
（Ⅱ）若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等，求四棱锥P-ABCD的体积．
已知等腰梯形ABCD的上底AB=3，下底CD=1，高DO=1．以高线DO为折痕，将平面ADO折起，使得平面ADO⊥平面BCDO，点H为棱AC的中点．
（1）求直线OC与直线AB所成的余弦值；
（2）求平面ADO与平面ACB所成的锐二面角的余弦值；
（3）在平面ADO内找一点G，使得GH⊥平面ACB．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网