��Ŀ����
14��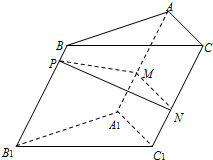 ��ͼ����PΪб������ABC-A1B1C1�IJ���BB1��һ�㣬PM��BB1��AA1�ڵ�M��PN��BB1��CC1�ڵ�N��
��ͼ����PΪб������ABC-A1B1C1�IJ���BB1��һ�㣬PM��BB1��AA1�ڵ�M��PN��BB1��CC1�ڵ�N����1����֤��CC1��MN��
��2���������DEF�������Ҷ�����DE2=DF2+EF2-2DF•EFcos��DFE����չ���ռ䣬��������ε����Ҷ�����д��б������������������������������������ɵĶ����֮��Ĺ�ϵʽ��������֤����
��3���ڣ�2���У����ǿ�����ƽ��ͼ���е�������ȵ��ռ�ͼ�ε����ӣ����������ӻ��в��٣�������۲�ƽ�湴�ɶ����������ͽ������������Ž����ɶ����ƹ㵽�ռ�ȥ��
| ���ɶ�������� | ������ABC | ������O-ABC |
| ���� | AB��AC | OA��OB��OC������ֱ |
| ���� | AB2+AC2=BC2 | �� |
���� ��1��������������������ʣ�֤�� CC1��ƽ��PMN����֤ CC1��MN��
��2��������������ߡ���Ӧ����������ó����ۣ�֤���õ����Ҷ���ƽ���ı��ε������ʽ�����еĴ�ֱ��ϵ��
��3����OH��ƽ��ABC������ΪH����HΪ��ABC�Ĵ��ģ�����CH���ӳ���AB��E������OE������OE��AB��֤��$S_{��OAB}^2=\frac{1}{4}A{B^2}•��EH•EC��=��\frac{1}{2}AB•EH��•��\frac{1}{2}AB•EC��={S_{��HAB}}•{S_{��CAB}}$��$S_{��OAC}^2={S_{��HAC}}•{S_{��BAC}}$��$S_{��OBC}^2={S_{��HBC}}•{S_{��ABC}}$�����ɵó����ۣ�
��� ��1��֤����������֪��CC1��BB1��PM��BB1��PN��BB1��
��CC1��PM��CC1��PN����PM��PN=P��
��CC1��ƽ��PMN��MN?ƽ��PMN��
��CC1��MN����4�֣�
��2���⣺��б������ABC-A1B1C1�У���$S_{AB{B_1}{A_1}}^2=S_{BC{C_1}{B_1}}^2+S_{AC{C_1}{A_1}}^2-2S_{BC{C_1}{B_1}}^{\;}•S_{AC{C_1}{A_1}}^{\;}cos��$
���Ц�Ϊƽ��CC1B1B��ƽ��CC1A1A����ɵĶ���ǣ���7�֣�
��CC1��ƽ��PMN���������Ķ����Ϊ��MNP��
�ڡ�PMN�У�PM2=PN2+MN2-2PN•MNcos��MNP
��PM2•CC12=PN2•CC12+MN2•CC12-2��PN•CC1��•��MN•CC1��cos��MNP��
��${S}_{BC{C}_{1}{B}_{1}}$=PN•CC1��${S}_{AC{C}_{1}{A}_{1}}$=MN•CC1��${S}_{AB{B}_{1}{A}_{1}}$=PM•BB1��
����$S_{AB{B_1}{A_1}}^2=S_{BC{C_1}{B_1}}^2+S_{AC{C_1}{A_1}}^2-2S_{BC{C_1}{B_1}}^{\;}•S_{AC{C_1}{A_1}}^{\;}cos��$����10�֣�
��3���ռ乴�ɶ����IJ��룺
��֪������O-ABC����������OA��OB��OC������ֱ������$S_{��OAB}^2+S_{��OAC}^2+S_{��OBC}^2=S_{��ABC}^2$��14�֣�
֤������OH��ƽ��ABC������ΪH����HΪ��ABC�Ĵ��ģ�
����CH���ӳ���AB��E������OE������OE��AB��
�ڡ�OAB�У�${S_{��OAB}}=\frac{1}{2}AB•OE⇒S_{��OAB}^2=\frac{1}{4}A{B^2}•O{E^2}$
��Rt��EOC�У�OE2=EH•EC��
��$S_{��OAB}^2=\frac{1}{4}A{B^2}•��EH•EC��=��\frac{1}{2}AB•EH��•��\frac{1}{2}AB•EC��={S_{��HAB}}•{S_{��CAB}}$
ͬ����$S_{��OAC}^2={S_{��HAC}}•{S_{��BAC}}$��$S_{��OBC}^2={S_{��HBC}}•{S_{��ABC}}$
����$S_{��OAB}^2+S_{��OAC}^2+S_{��OBC}^2=��{S_{��HAB}}+{S_{��HAC}}+{S_{��HBC}}��•{S_{��ABC}}=S_{��ABC}^2$��18�֣�
���� ���⿼�����洹ֱ��ϵ���ת���������������������֤������ʱ�������Ҷ����������ʵ��ı���֤�����ۣ�

�׳���
| ���� | [29.86�� 29.90 �� | [29.90�� 29.94�� | [29.94�� 29.98�� | [29.9 8�� 30.02�� | [30.02�� 30.06�� | [30.06�� 30.10�� | [30.10�� 30.14�� |
| Ƶ�� | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
| ���� | [29.86�� 29.90�� | [29.90�� 29.94�� | [29.94�� 29.98�� | [29.98�� 30.02�� | [30.02�� 30.06�� | [30.06�� 30.10�� | [30.10�� 30.14�� |
| Ƶ�� | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
��2��������ͳ������������2��2�������������Ƿ���99%�İ�����Ϊ�������ֳ�����������������в��족��
| �׳� | �ҳ� | �ϼ� | |
| ����Ʒ | |||
| ������Ʒ | |||
| �ϼ� |
| p��K2��k�� | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
| A�� | $-\frac{1}{2}{a^2}$ | B�� | $-\frac{{\sqrt{3}}}{2}{a^2}$ | C�� | $\frac{1}{2}{a^2}$ | D�� | $\frac{{\sqrt{3}}}{2}{a^2}$ |