题目内容
已知函数f(x)=sin(ωx+φ)(ω>0,-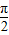 <φ<
<φ<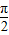 ),T=π,且f(x)满足对于任意x∈R都有f(
),T=π,且f(x)满足对于任意x∈R都有f(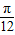 -x)=f(
-x)=f(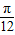 +x)
+x)(1)求ω、φ的值;
(2)写出函数的对称轴方程及对称中心的坐标.
【答案】分析:(1)由周期求出ω,由函数的对称轴方程求得φ的值.
(2)由(1)可得函数f(x)=sin(2x+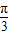 ),令2x+
),令2x+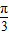 =kπ+
=kπ+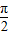 ,k∈z,求得对称轴方程.令2x+
,k∈z,求得对称轴方程.令2x+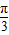 =kπ,k∈z,求得 x的值,可得对称中心的坐标.
=kπ,k∈z,求得 x的值,可得对称中心的坐标.
解答:解:(1)由于T=π=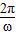 ,∴ω=2.再由f(x)满足对于任意x∈R都有f(
,∴ω=2.再由f(x)满足对于任意x∈R都有f(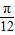 -x)=f(
-x)=f(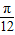 +x),故直线x=
+x),故直线x=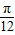 是函数图象的一条对称轴,
是函数图象的一条对称轴,
故有 2×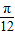 +φ=kπ+
+φ=kπ+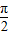 ,k∈z.
,k∈z.
再由-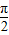 <φ<
<φ<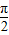 ,可得φ=
,可得φ=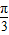 .
.
(2)由(1)可得函数f(x)=sin(2x+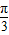 ),令2x+
),令2x+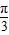 =kπ+
=kπ+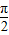 ,k∈z,可得 x=
,k∈z,可得 x=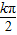 +
+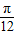 ,故对称轴方程为 x═
,故对称轴方程为 x═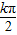 +
+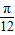 ,k∈z.
,k∈z.
令2x+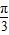 =kπ,k∈z,可得 x=
=kπ,k∈z,可得 x=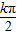 -
-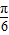 ,故对称中心的坐标为(
,故对称中心的坐标为( 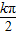 -
-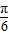 ,0),k∈z.
,0),k∈z.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,正弦函数的对称性,属于中档题.
(2)由(1)可得函数f(x)=sin(2x+
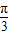 ),令2x+
),令2x+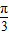 =kπ+
=kπ+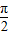 ,k∈z,求得对称轴方程.令2x+
,k∈z,求得对称轴方程.令2x+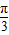 =kπ,k∈z,求得 x的值,可得对称中心的坐标.
=kπ,k∈z,求得 x的值,可得对称中心的坐标.解答:解:(1)由于T=π=
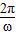 ,∴ω=2.再由f(x)满足对于任意x∈R都有f(
,∴ω=2.再由f(x)满足对于任意x∈R都有f(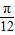 -x)=f(
-x)=f(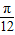 +x),故直线x=
+x),故直线x=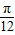 是函数图象的一条对称轴,
是函数图象的一条对称轴,故有 2×
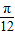 +φ=kπ+
+φ=kπ+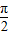 ,k∈z.
,k∈z.再由-
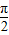 <φ<
<φ<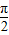 ,可得φ=
,可得φ=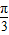 .
.(2)由(1)可得函数f(x)=sin(2x+
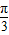 ),令2x+
),令2x+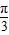 =kπ+
=kπ+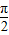 ,k∈z,可得 x=
,k∈z,可得 x=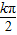 +
+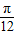 ,故对称轴方程为 x═
,故对称轴方程为 x═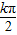 +
+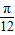 ,k∈z.
,k∈z.令2x+
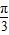 =kπ,k∈z,可得 x=
=kπ,k∈z,可得 x=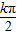 -
-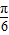 ,故对称中心的坐标为(
,故对称中心的坐标为( 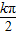 -
-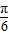 ,0),k∈z.
,0),k∈z.点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,正弦函数的对称性,属于中档题.

练习册系列答案
相关题目
