题目内容
矩形ABCD所在的平面与地面垂直，A点在地面上，AB=a，BC=b，AB与地面成θ(0≤θ≤| π |
| 2 |
分析：过B作直线与地面垂直，分别交过C、A的水平线于点E、F两点，分别在Rt△ABF和Rt△BCF中，利用三角函数的定义算出BF、BE的长，可得EF=asinθ+bcosθ，即可得到点C到地面的距离函数表达式．
解答：解：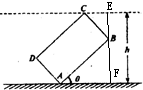
过B作直线与地面垂直，分别交过C、A的水平线于点E、F两点
则Rt△ABF中，∠BAF=θ，可得BF=ABsinθ=asinθ，
又∵Rt△BCF中，∠CBE=θ，
∴BE=BCcosθ=bcosθ
由此可得EF=BF+BE=asinθ+bcosθ
因此，点C到地面的距离为asinθ+bcosθ，即h（θ）=asinθ+bcosθ
故选：B
过B作直线与地面垂直，分别交过C、A的水平线于点E、F两点则Rt△ABF中，∠BAF=θ，可得BF=ABsinθ=asinθ，
又∵Rt△BCF中，∠CBE=θ，
∴BE=BCcosθ=bcosθ
由此可得EF=BF+BE=asinθ+bcosθ
因此，点C到地面的距离为asinθ+bcosθ，即h（θ）=asinθ+bcosθ
故选：B
点评：本题给出实际应用问题，求点C到地面的距离函数．着重考查了直角三角形中三角函数定义的知识，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
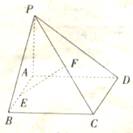（13分）如图3，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB，PC的中点。
（13分）如图3，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB，PC的中点。