题目内容
若复数z满足|z+4+3i|=3,则复数z的模应满足的不等式是( )A.5≤|z|≤8
B.2≤|z|≤8
C.|z|≤5
D.|z|<8
【答案】分析:设z=x+yi(x,y∈R),由已知中复数z满足|z+4+3i|=3,我们可得复数Z对应的点,在以(-4,3)为圆心,以3为半径的圆上,由复数|Z|= 表示(x,y)点到原点的距离,结合定点到定圆上动点间距离最值的求解方法,即可求出答案.
表示(x,y)点到原点的距离,结合定点到定圆上动点间距离最值的求解方法,即可求出答案.
解答:解:设z=x+yi(x,y∈R),
∵|z+4+3i|=3
∴(x+4)2+(y+3)2=9,
则(x,y)点表示以(-4,3)为圆心,以3为半径的圆
而复数|Z|= 表示(x,y)点到原点的距离,
表示(x,y)点到原点的距离,
由于(-4,3)到原点的距离为5,
故5-3≤|Z|≤5+3
即2≤|Z|≤8
故选B
点评:本题考查的知识点是复数求模,其中熟练掌握复数模的几何意义,将复数求模问题通过分析其几何意义转化为求定点到定圆上动点间距离最值问题是解答本题的关键.
 表示(x,y)点到原点的距离,结合定点到定圆上动点间距离最值的求解方法,即可求出答案.
表示(x,y)点到原点的距离,结合定点到定圆上动点间距离最值的求解方法,即可求出答案.解答:解:设z=x+yi(x,y∈R),
∵|z+4+3i|=3
∴(x+4)2+(y+3)2=9,
则(x,y)点表示以(-4,3)为圆心,以3为半径的圆
而复数|Z|=
 表示(x,y)点到原点的距离,
表示(x,y)点到原点的距离,由于(-4,3)到原点的距离为5,
故5-3≤|Z|≤5+3
即2≤|Z|≤8
故选B
点评:本题考查的知识点是复数求模,其中熟练掌握复数模的几何意义,将复数求模问题通过分析其几何意义转化为求定点到定圆上动点间距离最值问题是解答本题的关键.

练习册系列答案
相关题目
若复数z满足|z+4+3i|=3,则复数z的模应满足的不等式是( )
| A、5≤|z|≤8 | B、2≤|z|≤8 | C、|z|≤5 | D、|z|<8 |
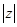 =( )
=( ) C.
C. D.
D.