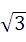题目内容
 为圆
为圆 :
: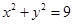 上任意一点,
上任意一点,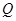 为圆
为圆 :
: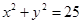 上任意一点,
上任意一点,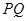 中
中
点组成的区域为 ,在
,在 内部任取一点,则该点落在区域
内部任取一点,则该点落在区域 上的概率为( )
上的概率为( )
A.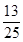 | B.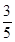 | C.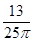 | D.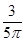 |
B
解析试题分析:【解析1】设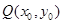 ,中点
,中点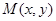 ,则
,则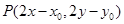 代入
代入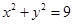 ,得
,得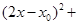
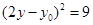 ,化简得:
,化简得: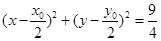 ,又
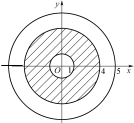
,又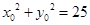 表示以原点为圆心半径为5的圆,故易知
表示以原点为圆心半径为5的圆,故易知 轨迹是在以
轨迹是在以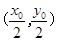 为圆心以
为圆心以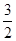 为半径的圆绕原点一周所形成的图形,即在以原点为圆心,宽度为3的圆环带上,即应有
为半径的圆绕原点一周所形成的图形,即在以原点为圆心,宽度为3的圆环带上,即应有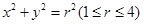 ,那么在
,那么在 内部任取一点落在
内部任取一点落在 内的概率
内的概率
为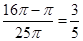 ,故选
,故选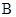 .
.

【解析2】设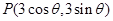 ,
,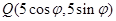 ,
,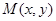 ,则
,则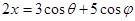 ,①
,①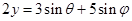 ,②,①2
,②,①2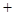 ②2得:
②2得: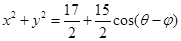
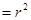 ,所以
,所以 的轨迹是以原点为圆心,以
的轨迹是以原点为圆心,以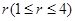 为半径的圆环,那么在
为半径的圆环,那么在 内部任取一点落在
内部任取一点落在 内的概率为
内的概率为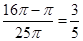 ,故选
,故选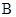 .
.
考点:几何概型.

练习册系列答案
相关题目
已知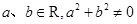 ,则直线
,则直线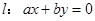 与圆:
与圆: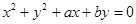 的位置关系是( ).
的位置关系是( ).
| A.相交 | B.相切 | C.相离 | D.不能确定 |
若直线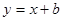 与曲线
与曲线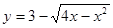 有公共点,则b的取值范围是 ( )
有公共点,则b的取值范围是 ( )
A.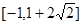 | B. |
C.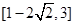 | D.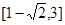 |
曲线f(x)=xlnx在点P(1,0)处的切线l与坐标轴围成的三角形的外接圆方程是( )
A.(x+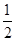 )2+(y- )2+(y-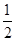 )2= )2=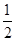 |
B.(x+1)2+(y-1)2=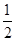 |
C.(x-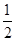 )2+(y+ )2+(y+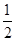 )2= )2=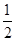 |
D.(x-1)2+(y+1)2=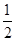 |
设圆 的一条切线与
的一条切线与 轴、
轴、 轴分别交于点
轴分别交于点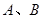 , 则
, 则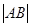 的最小值为( )
的最小值为( )
| A.4 | B.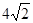 | C.6 | D.8 |
圆心在直线2x-3y-1=0上的圆与x轴交于A(1,0),B(3,0)两点,则圆的方程为( )
| A.(x-2)2+(y+1)2=2 |
| B.(x+2)2+(y-1)2=2 |
| C.(x-1)2+(y-2)2=2 |
| D.(x-2)2+(y-1)2=2 |
设过点(0,b)且斜率为1的直线与圆x2+y2+2x=0相切,则b的值为( )
A.2± | B.2±2 | C.1± | D. ±1 ±1 |
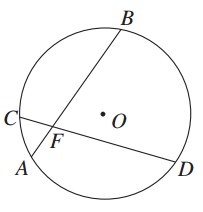
 B.2 C.3 D.2
B.2 C.3 D.2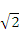 ,0)引直线ι与曲线
,0)引直线ι与曲线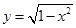 交于A,B两点 ,O为坐标原点,当△AOB的面积取最大值时,直线ι的斜率等于( )
交于A,B两点 ,O为坐标原点,当△AOB的面积取最大值时,直线ι的斜率等于( )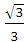 B.-
B.-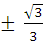 D-
D-