Question

（本小题满分12分）

如图1，在三棱锥P－A.BC中，PA.⊥平面A.BC，A.C⊥BC，D为侧棱PC上一点，它的正(主)视图和侧(左)视图如图2所示．

(1) 证明：A.D⊥平面PBC；

(2) 求三棱锥D－A.BC的体积；

(3) 在∠A.CB的平分线上确定一点Q，使得PQ∥平面A.BD，并求此时PQ的长．

 

Answer 1

【答案】

（1）见解析

(2)   ;

(3)

【解析】本题考查由三视图求面积、体积，直线与平面平行的性质，直线与平面垂直的判定，考查空间想象能力，逻辑思维能力，计算能力，是中档题

（Ⅰ）证明AD垂直平面PBC内的两条相交直线PC、BC，即可证明AD⊥平面PBC；

（Ⅱ）求出三棱锥的底面ABC的面积，求出高BC，再求三棱锥D-ABC的体积；

（Ⅲ）取AB的中点O，连接CO并延长至Q，使得CQ=2CO，点Q即为所求，证明PQ平行平面ABD内的直线OD，即可证明PQ∥平面ABD，在直角△PAQ中，求此时PQ的长．

(2)      

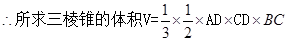
…… 8分

(3)取A.B的中点O，连接CO并延长至Q，使得CQ＝2CO，连接PQ，OD，点Q即为所求．

因为O为CQ的中点，D为PC的中点，  PQ∥OD,

 PQ平面A.BD, OD平面A.BD        PQ∥平面A.BD

连接A.Q,BQ,

四边形A.CBQ的对角线互相平分， 且A.C=BC,A.CBC,   

四边形A.CBQ为正方形，CQ即为∠A.CB的平分线       

又A.Q=4，PA.平面A.BC