题目内容
求证：平行四边形对角线的平方和等于四边的平方和.
证法一:如图，ABCD中，求证：AB2+BC2+CD2+DA2=AC2+BD2.
设
=b, 
=a,AC2=|
|2=(a+b)2=a2+b2+
BD2=|
|2=(a-b)2=a2+b2
①+②得
AC2+BD2=
故原命题得证.
证法二:如图，建立直角坐标系，设A（m,n),C(p,0),
则
=（m,n).
∴D(p+m,n).
∴有AB2=CD2=
=m2+n2,DA2=BC2=
=p2.
∴有AB2+BC2+CD2+DA2=2（m2+n2+p2).
又∵BD2=
=（p+m)2+n2,
AC2=
=(m-p)2+n2,
∴有BD2+AC2=（p+m)2+n2+(m-p)2+n2=2(p2+m2+n2).
∴原命题成立.
练习册系列答案
相关题目
三棱锥A-BCD中，对棱AD、BC所成的角为30°且AD=BC=a．截面EFGH是平行四边形，交AB、AC、CD、BD于E、F、G、H，设
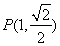
的中心在坐标原点，焦点在
轴上，椭圆上的点到
，离心率
.
、
，过点
的直线
与该椭圆交于点
、
, 
、
为邻边作平行四边形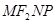
，求该平行四边形对角线
的长度