题目内容
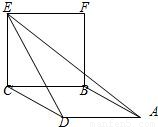
如图,ABCD为菱形,CEFB为正方形,平面ABCD⊥平面CEFB,CE=1,∠AED=30°,则异面直线BC与AE所成角的大小为
______度.

解析:由题意,正方形和菱形变成均为1,
又平面ABCD⊥平面CEFB,所以CE⊥平面ABCD
于是CE⊥CD,从而DE=
在△ADE中,AD=1,DE=
,∠AED=30°
由正弦定理得:
=
所以sin∠DAE=
=
故∠DAE=45°
又BC∥AD,故异面直线BC与AE所成角等于∠DAE
故答案为:45°
又平面ABCD⊥平面CEFB,所以CE⊥平面ABCD
于是CE⊥CD,从而DE=
| 2 |
在△ADE中,AD=1,DE=
| 2 |
由正弦定理得:
| AD |
| sin∠AED |
| DE |
| sin∠DAE |
所以sin∠DAE=
| DE?sin∠AED |
| AD |
| ||
| 2 |
故∠DAE=45°
又BC∥AD,故异面直线BC与AE所成角等于∠DAE
故答案为:45°

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
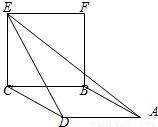
 如图,ABCD为菱形,CEFB为正方形,平面ABCD⊥平面CEFB,CE=1,∠AED=30°,则异面直线BC与AE所成角的大小为
如图,ABCD为菱形,CEFB为正方形,平面ABCD⊥平面CEFB,CE=1,∠AED=30°,则异面直线BC与AE所成角的大小为