题目内容

已知函数y=Asin（ωx+φ） （x∈R；A＞0；ω＞0；|φ|＜
π
2
） 该函数图象上的一个最高点坐标为（
π
6
，3），与其相邻的对称中心的坐标是（-
π
12
，0），求该函数y=Asin（ωx+φ）的解析式．
因为函数y=Asin（ωx+φ） （x∈R；A＞0；ω＞0；|φ|＜
π
2
），
该函数图象上的一个最高点坐标为（
π
6
，3），
所以A=3，
与其相邻的对称中心的坐标是（-
π
12
，0），所以T=4×(
π
6
+
π
12
)=π，所以ω=2，
函数y=3sin（2x+φ）经过（
π
6
，3），3=3sin（2×
π
6
+φ），|φ|＜
π
2
，所以φ=
π
6
．
该函数y=Asin（ωx+φ）的解析式：y=3sin（2x+
π
6
）．
练习册系列答案
相关题目
已知函数y=Asin（ωx+φ），在同一周期内，当x=
π
12
时，取最大值y=2，当x=
7π
12
时，取得最小值y=-2，那么函数的解析式为（　　）
A、y=
1
2
sin（x+
π
3
）
B、y=2sin（2x+
π
3
）
C、y=2sin（
x
2
-
π
6
）
D、y=2sin（2x+
π
6
）
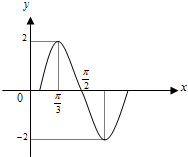精英家教网已知函数y=Asin（ωx+∅）（A＞0，ω＞0，-π≤∅≤π）一个周期的图象（如图），则这个函数的一个解析式为（　　）
A、y=2sin(
3
2
x+
π
2
)
B、y=2sin(3x+
π
6
)
C、y=2sin(3x-
π
6
)
D、y=2sin(3x-
π
2
)
已知函数y=Asin(ωx+?)+B(A＞0，ω＞0，|?|＜
π
2
)的周期为T，在一个周期内的图象如图所示，则φ=
-
π
6
-
π
6
．
已知函数y=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜
π
2
)的一部分图象如图所示，则（　　）
已知函数y=Asin（ωx+∅）+k的最大值为4，最小值为0，最小正周期是
π
2
，在x∈[
π
24
，
π
12
]上单调递增，则下列符合条件的解析式是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网