题目内容
已知数列{an}满足:a1=2t-3(t∈R且t≠±1),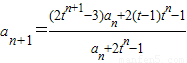 (n∈N*).
(n∈N*).(1)当t=2时,求证:
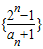 是等差数列;
是等差数列;(2)若t>0,试比较an+1与an的大小;
(3)在(2)的条件下,已知函数f(x)=
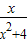 (x>0),是否存在正整数t,使得对一切n∈N*不等式f(an+1)<f(an)恒成立?若存在,求出t的最小值;若不存在,请说明理由.
(x>0),是否存在正整数t,使得对一切n∈N*不等式f(an+1)<f(an)恒成立?若存在,求出t的最小值;若不存在,请说明理由.
【答案】分析:(1)利用数列递推式,化简,可得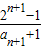 -
-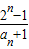 =
= ,从而
,从而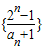 是以
是以 为公差的等差数列;
为公差的等差数列;
(2)先确定数列的通项,再利用作差比较法,即可得到结论;
(3)对一切n∈N*不等式f(an+1)<f(an)恒成立,可转化为an+1an-4>0,{an}为递增数列,只需a1a2-4>0,由此可得结论.
解答:(1)证明:当t=2时,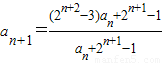
∴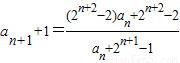
∴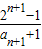 =
=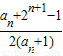
∴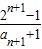 -
-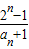 =
=
∴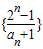 是以
是以 为公差的等差数列;
为公差的等差数列;
(2)解:∵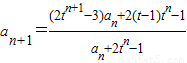 =
=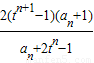
∴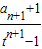 =
=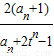 =
=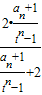
令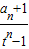 =bn,则bn+1=
=bn,则bn+1=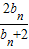 ,b1=
,b1=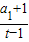 =2
=2
∴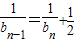 ,
,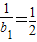
∴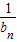 =
=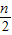
∴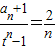
∴an=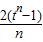
∴an+1-an=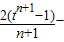
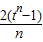 =
=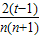 [n(1+t+…+tn)-(n+1)(1+t+…+tn-1)]
[n(1+t+…+tn)-(n+1)(1+t+…+tn-1)]
=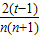 [(tn-1)+…+(tn-tn-1)]=
[(tn-1)+…+(tn-tn-1)]=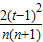 [(1+t+…+tn-1)+t(1+t+…+tn-2)+…+tn-1]
[(1+t+…+tn-1)+t(1+t+…+tn-2)+…+tn-1]
显然t>0(t≠1)时,an+1-an>0,∴an+1>an;
(3)解:∵f(an+1)-f(an)=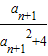 -
-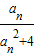 =
=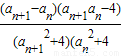 <0,an+1>an
<0,an+1>an
∴an+1an-4>0,{an}为递增数列
∴只需a1a2-4>0
∴(2t-3)(t2-2)-4>0
令f(t)=(2t-3)(t2-2)-4,则f′(t)=6t2-6t-8
∴t>2时,f′(t)>0,函数为增函数
∵f(2)=-2<0,f(3)=17>0
∴满足题意的最小正整数t存在,最小值为3.
点评:本题考查数列递推式,考查数列的通项,考查学生分析解决问题的能力,难度较大.
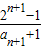 -
-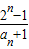 =
= ,从而
,从而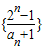 是以
是以 为公差的等差数列;
为公差的等差数列;(2)先确定数列的通项,再利用作差比较法,即可得到结论;
(3)对一切n∈N*不等式f(an+1)<f(an)恒成立,可转化为an+1an-4>0,{an}为递增数列,只需a1a2-4>0,由此可得结论.
解答:(1)证明:当t=2时,
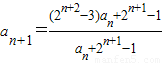
∴
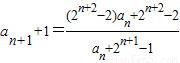
∴
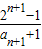 =
=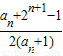
∴
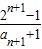 -
-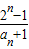 =
=
∴
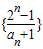 是以
是以 为公差的等差数列;
为公差的等差数列;(2)解:∵
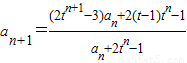 =
=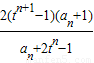
∴
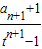 =
=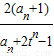 =
=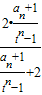
令
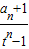 =bn,则bn+1=
=bn,则bn+1=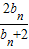 ,b1=
,b1=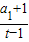 =2
=2∴
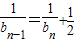 ,
,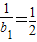
∴
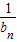 =
=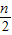
∴
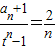
∴an=
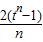
∴an+1-an=
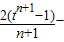
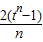 =
=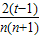 [n(1+t+…+tn)-(n+1)(1+t+…+tn-1)]
[n(1+t+…+tn)-(n+1)(1+t+…+tn-1)]=
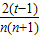 [(tn-1)+…+(tn-tn-1)]=
[(tn-1)+…+(tn-tn-1)]=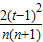 [(1+t+…+tn-1)+t(1+t+…+tn-2)+…+tn-1]
[(1+t+…+tn-1)+t(1+t+…+tn-2)+…+tn-1]显然t>0(t≠1)时,an+1-an>0,∴an+1>an;
(3)解:∵f(an+1)-f(an)=
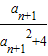 -
-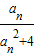 =
=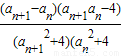 <0,an+1>an
<0,an+1>an∴an+1an-4>0,{an}为递增数列
∴只需a1a2-4>0
∴(2t-3)(t2-2)-4>0
令f(t)=(2t-3)(t2-2)-4,则f′(t)=6t2-6t-8
∴t>2时,f′(t)>0,函数为增函数
∵f(2)=-2<0,f(3)=17>0
∴满足题意的最小正整数t存在,最小值为3.
点评:本题考查数列递推式,考查数列的通项,考查学生分析解决问题的能力,难度较大.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目