题目内容
若集合A={y|y=(
)x}，B={y|y=2-
}，则A∩B等于（ ）
| 1 |
| 3 |
| 1 |
| x |
分析：先利用求函数的值域的方法化简集合A，B，后求它们的交集．
解答：解：∵A={y|y=(
)x}={y|y＞0}，
∵B={y|y=2-
}={y|y≠2}，
∴A∩B=（0，2）∪（2，+∞）．
故选C．
| 1 |
| 3 |
∵B={y|y=2-
| 1 |
| x |
∴A∩B=（0，2）∪（2，+∞）．
故选C．
点评：集合中的运算包括集合之间的子集、交集、并集和补集运算．这类集合问题都是以基本题的身份出现在高考试卷中，解答时应正确地掌握集合的概念，理解集合的含义，将集合等价变形，利用数轴或韦恩图进一步研究集合的运算．
练习册系列答案
孟建平名校考卷系列答案
相关题目
若集合A={y|y=x3，0≤x≤1}，集合B={y|y=
，0＜x≤1}，则A∩CRB等于（ ）
| 1 |
| x |
| A、[0，1] | B、[0，1） |
| C、（1，+∞） | D、{1} |
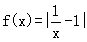
上的单调性，并证明你的结论；
}，B=[0,1]， 试判断A与B的关系；
}，B={y|y=3-x}，则A∪B=（ ）