题目内容
【题目】选修4一4:坐标系与参数方程
已知曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出![]() 的极坐标方程和
的极坐标方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 的极坐标分别为
的极坐标分别为![]() 和
和![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,射线
两点,射线![]()
与曲线![]() 相交于点
相交于点![]() ,射线
,射线![]() 与曲线
与曲线![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ,
, ![]() (2)
(2)![]()
【解析】试题分析:(1)利用cos2θ+sin2θ=1,即可曲线C1的参数方程化为普通方程,进而利用![]() 即可化为极坐标方程,同理可得曲线C2的直角坐标方程;
即可化为极坐标方程,同理可得曲线C2的直角坐标方程;
(2)由点M1、M2的极坐标可得直角坐标:M1(0,1),M2(2,0),可得直线M1M2的方程为![]() 此直线经过圆心,可得线段PQ是圆x2+(y-1)2=1的一条直径,可得得OA⊥OB,A,B是椭圆
此直线经过圆心,可得线段PQ是圆x2+(y-1)2=1的一条直径,可得得OA⊥OB,A,B是椭圆![]() 上的两点,在极坐标下,设A(ρ1,θ),B(ρ2,θ+
上的两点,在极坐标下,设A(ρ1,θ),B(ρ2,θ+![]() ) 代入椭圆的方程即可得解.
) 代入椭圆的方程即可得解.
试题解析:
(1)曲线![]() 的普通方程为
的普通方程为![]() ,化成极坐标方程为
,化成极坐标方程为![]()
曲线![]() 的直角坐标方程为
的直角坐标方程为![]()
(2)在直角坐标系下, ![]() ,可得直线M1M2的方程为
,可得直线M1M2的方程为![]() 此直线经过圆心,可得线段
此直线经过圆心,可得线段![]() 是圆
是圆![]() 的直径
的直径
∴![]() 由
由![]() 得
得![]() ,
, ![]() 是椭圆
是椭圆![]() 上的两点,在极坐标下,设
上的两点,在极坐标下,设
![]() 分别代入
分别代入![]() 中,
中,
有![]() 和
和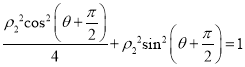
∴![]()
则![]() ,即
,即![]() .
.

练习册系列答案
相关题目