题目内容
过点P(2,3)和Q(-1,6)的直线PQ的倾斜角为 .
【答案】分析:由经过两点直线的斜率公式,得PQ的斜率为-1,再根据斜率k与倾斜角α的关系,得tanα=-1,结合直线倾斜角的取值范围即可得到直线PQ的倾斜角.
解答:解:∵点P坐标为(2,3),点Q坐标为(-1,6)
∴直线PQ的斜率为k=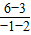 =-1
=-1
设直线的倾斜角为α,则tanα=-1
∵α∈[0,π),∴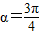
故答案为: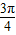
点评:本题给出直角坐标系中两个定点,求它们确定直线的倾斜角.着重考查了直线的斜率公式和斜率与倾斜角的关系等知识,属于基础题.
解答:解:∵点P坐标为(2,3),点Q坐标为(-1,6)
∴直线PQ的斜率为k=
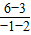 =-1
=-1设直线的倾斜角为α,则tanα=-1
∵α∈[0,π),∴
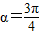
故答案为:
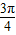
点评:本题给出直角坐标系中两个定点,求它们确定直线的倾斜角.着重考查了直线的斜率公式和斜率与倾斜角的关系等知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目