题目内容
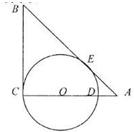已知△ABC中，∠ACB=90°，O是AC上一点，以O为圆心，OC为半径的圆交AC于D，与AB切于E，若AD=2，AE=4，求BE的长．
分析：法一、由圆O与AB切于E，根据切割线定理，我们根据AD=2，AE=4，得到AC的值，进一步求出圆O的半径，连接OE后，易得△AEO∽△ACB，然后根据相似三角形的性质，我们不难得到BE的长．
法二、在求出AC的值后，设BE长为x，然后根据过圆外一点到圆的两条切线长相等，构造关于x的方程，然后解方程即可得到BE的长．
法二、在求出AC的值后，设BE长为x，然后根据过圆外一点到圆的两条切线长相等，构造关于x的方程，然后解方程即可得到BE的长．
解答：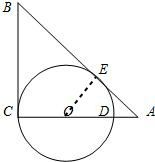
解：法一：圆O与AB切于E，
由切割线定理得AE2=AD•AC，
∴AC=8
∵圆的半径OD=
(AC-AD)=3
连接OE，则OE⊥AB
∠AEO=∠ACB=90°
∠OAE=∠BAC
∴△AEO∽△ACB
=
∴AB=10
BE=AB-AE=6．
法二：圆O与AB切于E，
由切割线定理得AE2=AD•AC，
∴AC=8
∵BE，BC都是圆O的切线
∴BE=BC=x
在Rt△ABC中，BC2+AC2=AB2
∴x2+82=（x+4）2
∴x=6
即BE=6．
解：法一：圆O与AB切于E，由切割线定理得AE2=AD•AC，
∴AC=8
∵圆的半径OD=
| 1 |
| 2 |
连接OE，则OE⊥AB
∠AEO=∠ACB=90°
∠OAE=∠BAC
∴△AEO∽△ACB
| AE |
| AO |
| AC |
| AB |
∴AB=10
BE=AB-AE=6．
法二：圆O与AB切于E，
由切割线定理得AE2=AD•AC，
∴AC=8
∵BE，BC都是圆O的切线
∴BE=BC=x
在Rt△ABC中，BC2+AC2=AB2
∴x2+82=（x+4）2
∴x=6
即BE=6．
点评：要求线段的长度，我们要先分析已知线段与待求线段之间的关系，在分析过程中要善于分析已知条件及已知条件中隐含的数量关系，然后根据分析过程，利用相似三角形的性质、与圆相关的比例线段等，列出相关的式子，进行求解．
练习册系列答案
相关题目