题目内容
 如图,函数y=f(x)的图象在点P处的切线是l,则f(2)+f′(2)=
如图,函数y=f(x)的图象在点P处的切线是l,则f(2)+f′(2)=分析:本题根据导数的基本运算结合函数图象可计算出f′(x)的式子,进而可求出y=f(X)的式子,即可求得结果.
解答:解:由图象可得:函数y=f(x)的图象在点P处的切线是l与x轴交与(4,0),与y轴交于(0,4),则可知
l:x+y=4,∴f(2)=2,f′(2)=-1
∴代入则可得f(2)+f′(2)=1,
故答案为:1.
l:x+y=4,∴f(2)=2,f′(2)=-1
∴代入则可得f(2)+f′(2)=1,
故答案为:1.
点评:本题考查导数性质的基本应用,结合图形的基本性质即可求得答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
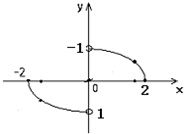 如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{
| ||||||||
B、{x|-2≤x<
| ||||||||
C、{x|-
| ||||||||
D、{x|-
|
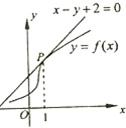 8、如图,函数y=f(x)的图象在点P处的切线方程为x-y+2=0,则f(1)+f′(1)=( )
8、如图,函数y=f(x)的图象在点P处的切线方程为x-y+2=0,则f(1)+f′(1)=( )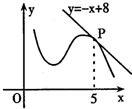 (文)如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=
(文)如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)= (2012•茂名一模)如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
(2012•茂名一模)如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: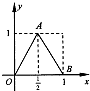 (2013•金华模拟)如图,函数y=f(x)的图象为折线OAB,设g(x)=f[f(x)],则满足方程g(x)=x的根的个数为( )
(2013•金华模拟)如图,函数y=f(x)的图象为折线OAB,设g(x)=f[f(x)],则满足方程g(x)=x的根的个数为( )