题目内容
8.已知在平面直角坐标系中,圆C的方程为x2+y2-4x+2y+4=0,若圆心C到直线y=kx+2的距离不大于圆的直径,则实数k的取值范围是k≤$\frac{9}{2}$.分析 将圆C的方程整理为标准形式,找出圆心C的坐标与半径r,根据圆心C到直线y=kx+2的距离不大于圆的直径,利用点到直线的距离公式列出关于k的不等式求出不等式的解集即可得到k的范围.
解答 解:将圆C的方程整理为标准方程得:(x-2)2+(y+1)2=1,
∴圆心C(2,-1),半径r=1,
∵圆心C到直线y=kx+2的距离不大于圆的直径,
∴$\frac{|2k+3|}{\sqrt{{k}^{2}+1}}$≤2,
∴k≤$\frac{9}{2}$.
故答案为:k≤$\frac{9}{2}$.
点评 此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,考查学生的计算能力,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
20.$\sqrt{1-co{s}^{2}\frac{π}{5}}$=( )
| A. | sin$\frac{π}{5}$ | B. | cos$\frac{π}{5}$ | C. | -sin$\frac{π}{5}$ | D. | -cos$\frac{π}{5}$ |
 是圆
是圆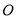 的直径,点
的直径,点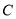 是圆
是圆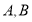 的点,
的点,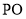 垂直于圆
垂直于圆 所在的平面,且
所在的平面,且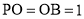 .
.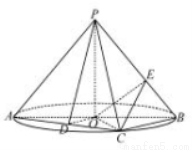
 为线段
为线段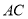 的中点,求证
的中点,求证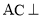 平面
平面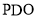 ;
;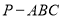 体积的最大值;
体积的最大值;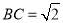 ,点
,点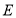 在线段
在线段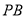 上,求
上,求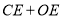 的最小值.
的最小值.