题目内容

已知奇函数f（x）定义域是（-2，2），且在定义域上单调递减，若f（2-a）+f（2a-3）＜0，则a的取值范围是

A.
（0，4）
B.
$数学公式$
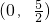
C.
$数学公式$
D.
$数学公式$

D
分析：由f（2-a）+f（2a-3）＜0，结合已知条件可得-2＜3-2a＜2-a＜2，解不等式可求a的范围
解答：∵函数函数f（x）定义域在（-2，2）上的奇函数
则由f（2-a）+f（2a-3）＜0，可得f（2-a）＜-f（2a-3）=f（3-2a）
函数在定义域上单调递减
∴-2＜3-2a＜2-a＜2
∴ $\text{[math]}$
解可得， $\text{[math]}$
∴ $\text{[math]}$
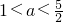
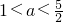
故选D
点评：本题主要考查了函数的奇偶性及函数的单调性在抽象函数中的应用，及不等式的求解，属于基础试题

练习册系列答案

黄冈经典阅读系列答案

文言文课外阅读特训系列答案

轻松阅读训练系列答案

南大教辅初中英语任务型阅读与首字母填空系列答案

初中英语听力与阅读系列答案

领航英语阅读理解与完形填空系列答案

英语拓展听力与阅读系列答案

阅读组合突破系列答案

初中英语阅读系列答案

全程探究阅读系列答案

相关题目

（2009•天门模拟）已知命题：
①函数f（x）=

在（0，+∞）上是减函数；
②已知

=（3，4），

=（0，-1），则

方向上的投影为-4；
③函数f（x）=2sinxcos|x|的最小正周期为π；
④函数f（x）的定义域为R，则f（x）是奇函数的充要条件是f（0）=0；
⑤在平面上，到定点（2，1）的距离与到定直线3x+4y-10的距离相等的点的轨迹是抛物线．
其中，正确命题的序号是

．（写出所有正确命题的序号）．

已知函数y＝f(x)是偶函数，y＝g(x)是奇函数，它们的定域[－π，π]，且它们在x∈[0，π]上的图象如图所示，则不等式＜0的解集是________．

已知命题：
①函数f（x）=

在（0，+∞）上是减函数；
②已知

=（3，4），

=（0，-1），则

方向上的投影为-4；
③函数f（x）=2sinxcos|x|的最小正周期为π；
④函数f（x）的定义域为R，则f（x）是奇函数的充要条件是f（0）=0；
⑤在平面上，到定点（2，1）的距离与到定直线3x+4y-10的距离相等的点的轨迹是抛物线．
其中，正确命题的序号是______．（写出所有正确命题的序号）．