题目内容
(本小题满分13分)已知函数
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当 时,讨论
时,讨论 的单调性.
的单调性.
(Ⅰ)
(Ⅱ)当 时,
时, 在
在 单调递减,
单调递减, 在
在 单调递增;
单调递增;
当 时,
时,  在
在 单调递减,
单调递减, 在
在 单调递增;
单调递增;
当 时
时 在
在 单调递减.
单调递减.
【解析】
试题分析:(Ⅰ)利用导数的几何意义求曲线在点 处的切线方程,注意这个点的切点. (Ⅱ)函数的单调性与导数之间的关系
处的切线方程,注意这个点的切点. (Ⅱ)函数的单调性与导数之间的关系 且不恒为0时单调递增,
且不恒为0时单调递增, 且不恒为0时单调递减,如果有字母系数,要注意分类讨论
且不恒为0时单调递减,如果有字母系数,要注意分类讨论
试题解析:(Ⅰ)当 时,
时, ,此时
,此时 , 2分
, 2分
 ,又
,又 ,
,
所以切线方程为: ,
,
整理得: ;
;  分
分
(Ⅱ) , 6分
, 6分
当 时,
时, ,此时,在
,此时,在 上
上 ,
, 单调递减,
单调递减,
在 上
上 ,
, 单调递增; 8分
单调递增; 8分
当 时,
时, ,
,
当 ,即
,即 时
时 在
在 恒成立,
恒成立,
所以 在
在 单调递减; 10分
单调递减; 10分
当 时,
时, ,此时在
,此时在 上
上 ,
, 单调递减,
单调递减,
 在
在 上
上 单调递增; 12分
单调递增; 12分
综上所述:当 时,
时, 在
在 单调递减,
单调递减, 在
在 单调递增;
单调递增;
当 时,
时,  在
在 单调递减,
单调递减, 在
在 单调递增;
单调递增;
当 时
时 在
在 单调递减. 13分
单调递减. 13分
考点:(1)利用导数求切线方程;(2)利用导数研究函数的单调性.

练习册系列答案
相关题目
 ,则“
,则“ ”是“
”是“ 恒成立”的( )
恒成立”的( )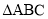 中,“
中,“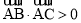 ”是“
”是“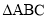 为锐角三角形”的( )
为锐角三角形”的( ) (
( )的准线与圆
)的准线与圆 相切,则
相切,则 的值为 .
的值为 . (
( ,
, ,
, )的部分图象如图所示,则
)的部分图象如图所示,则 ( )
( )
 B.
B. C.
C. D.
D.

 _______.
_______.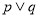 为真”是“
为真”是“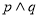 为真”的充分不必要条件;
为真”的充分不必要条件;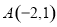 在抛物线
在抛物线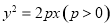 的准线上,记其焦点为F,则直线AF的斜率等于
的准线上,记其焦点为F,则直线AF的斜率等于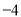
 ,则变量
,则变量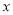 每增加一个单位,
每增加一个单位,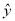 平均减少1.5个单位;
平均减少1.5个单位; 满足约束条件
满足约束条件 的最小值为
的最小值为 ,则
,则 =_________.
=_________.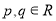 ,则“
,则“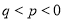 ”是“
”是“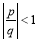 ”的
”的