题目内容
如图，在Rt△ABC中，已知BC=a，若长为2a的线段PQ以点A为中点，问| PQ |
| BC |
| BP |
| CQ |
分析：要求
与
的夹角θ取何值时
•
的值最大，我们有两种思路：
法一：是将向量
与
根据向量加减法的三角形法则，进行分析，分解成用向量
、
、
、
表示的形式，然后根据|
|=|
|=a，
⊥
即
•
=0，构造一个关于cosθ的式子，然后根据cosθ的取值范围，分析出
•
的最大值；
法二：是以直角顶点A为坐标原点，两直角边所在直线为坐标轴建立如图所示的平面直角坐标系．求出各顶点的坐标后，进而给出向量
与
的坐标，然后利用平面向量的数量值运算公式，构造一个关于cosθ的式子，然后根据cosθ的取值范围，分析出
•
的最大值．
| PQ |
| BC |
| BP |
| CQ |
法一：是将向量
| PQ |
| BC |
| AP |
| AQ |
| AC |
| AB |
| AP |
| AQ |
| AC |
| AB |
| AC |
| AB |
| BP |
| CQ |
法二：是以直角顶点A为坐标原点，两直角边所在直线为坐标轴建立如图所示的平面直角坐标系．求出各顶点的坐标后，进而给出向量
| BP |
| CQ |
| BP |
| CQ |
解答：
解：如下图所示：
解法一：∵
⊥
，∴
•
=0．
∵
=-
，
=
-
，
=
-
，
∴
•
=(
-
)•(
-
)
=
•
-
•
-
•
+
•
=-a2-
•
+
•
=-a2+
•
=-a2+a2cosθ．
故当cosθ=1，即θ=0（
与
方向相同）时，
•
最大．其最大值为0．
解法二：以直角顶点A为坐标原点，两直角边所在直线为坐标轴建立如图所示的平面直角坐标系．
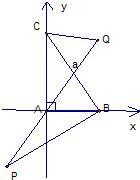设|AB|=c|AC|=b，则A（0，0），B（c，0），C（0，b），
且|PQ|=2a，|BC|=a．
设点P的坐标为（x，y），则Q（-x，-y）．
∴
=(x-c，y)，
=(-x，-y-b)，
=(-c，b)，
=(-2x，-2y)．
∴
•
=(x-c)(-x)+y(-y-b)
=-（x2+y2）+cx-by．
∵cosθ=
=
．
∴cx-by=a2cosθ．
∴
•
=-a2+a2cosθ．
故当cosθ=1，
即θ=0（
与
方向相同）时，
•
最大，其最大值为0．
解：如下图所示：解法一：∵
| AB |
| AC |
| AB |
| AC |
∵
| AP |
| AQ |
| BP |
| AP |
| AB |
| CQ |
| AQ |
| AC |
∴
| BP |
| CQ |
| AP |
| AB |
| AQ |
| AC |
=
| AP |
| AQ |
| AP |
| AC |
| AB |
| AQ |
| AB |
| AC |
=-a2-
| AP |
| AC |
| AB |
| AP |
=-a2+
| 1 |
| 2 |
| PQ |
| BC |
=-a2+a2cosθ．
故当cosθ=1，即θ=0（
| PQ |
| BC |
| BP |
| CQ |
解法二：以直角顶点A为坐标原点，两直角边所在直线为坐标轴建立如图所示的平面直角坐标系．
设|AB|=c|AC|=b，则A（0，0），B（c，0），C（0，b），且|PQ|=2a，|BC|=a．
设点P的坐标为（x，y），则Q（-x，-y）．
∴
| BP |
| CQ |
| BC |
| PQ |
∴
| BP |
| CQ |
=-（x2+y2）+cx-by．
∵cosθ=
| ||||
|
|
| cx-by |
| a2 |
∴cx-by=a2cosθ．
∴
| BP |
| CQ |
故当cosθ=1，
即θ=0（
| PQ |
| BC |
| BC |
| CQ |
点评：本小题主要考查向量的概念，平面向量的运算法则，考查运用向量及函数知识的能力．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠C=90°，D为BC上一点，∠DAC=30°，BD=2，AB=2| 3 |
A、2
| ||||
| B、3 | ||||
C、
| ||||
D、
|
如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E．
如图，在Rt△ABC中，∠ABC=90°，BA=BC=2，AE⊥平面ABC，CD⊥平面ABC，CE交AD于点P．
8．如图，在Rt△ABC中，∠CAB=90°，AB=2，AC=
如图，在Rt△ABC中，AC=1，BC=x，D是斜边AB的中点，将△BCD沿直线CD翻折，若在翻折过程中存在某个位置，使得CB⊥AD，则x的取值范围是（ ）A、（0，
| ||||
B、（
| ||||
C、（
| ||||
| D、（2，4] |