题目内容
如图，四棱锥P－A
BCD的底面是正方形，PD⊥底面ABCD，点E在棱PB上．
(1)求证：平面AEC⊥平面PDB；
(2)若E为PB的中点，棱PC(不包括端点)
上是否存在点F，使得DF∥平面AEC，若存在，找出点F的位置，若不存在，说明理由．
解：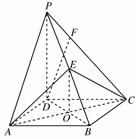
(1)证明：∵四边形ABCD是正方形，∴AC⊥BD，
∵PD⊥底面ABCD，
∴PD⊥AC，∴AC⊥平面PDB，
又AC⊂平面AEC，
∴平面AEC⊥平面PDB.
(2)不存在这样的点．
假设存在点F，使DF∥平面AEC.
设BD与AC交于点O，则O是BD的中点，
由于点E是PB的中点，所以PD∥EO，
又EO⊂平面AEC.PD⊄平面AEC，故PD∥平面AEC.
根据假设DF∥平面AEC
.
因为DF⊂平面PDC，PD⊂平面PDC，PD∩DF＝D，
所以平面PDC∥平面AEC，但平面PDC与平面AEC有公共点C，两平面相交，矛盾，故假设不成立，即不存在这样的点F，使得DF∥平面AEC.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，CE∥AB．
如图，四棱锥P-ABCD的底面ABCD是正方形，AC∩BD=O，PA⊥底面ABCD，OE⊥PC于E．
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PD⊥平面ABCD，点E，F分别是AB和PC的中点．
如图，四棱锥P-ABCD，PA⊥底面ABCD，AB∥CD，AB⊥AD，AB=AD=