题目内容
下列函数中,在其定义域内既是奇函数,又是增函数的函数是
- A.f(x)=-x3
- B.
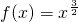
- C.f(x)=x|x|
- D.f(x)=-x-3
C
分析:对于A,函数是奇函数,但是减函数;对于B,函数非奇非偶,不满足题意;对于C,f(-x)=-x|-x|=-x|x|=-f(x),是奇函数,又 ,故是R上的增函数;对于D,函数是奇函数,但是增函数.
,故是R上的增函数;对于D,函数是奇函数,但是增函数.
解答:由题意,对于A,函数是奇函数,但是减函数,故不满足题意;
对于B,函数非奇非偶,不满足题意;
对于C,f(-x)=-x|-x|=-x|x|=-f(x),是奇函数,又 ,故是R上的增函数,故满足题意
,故是R上的增函数,故满足题意
对于D,函数是奇函数,但是增函数,故不满足题意;
故选C.
点评:本题考查函数单调性与奇偶性的综合,解题的依据是函数单调性与奇偶性的定义.
分析:对于A,函数是奇函数,但是减函数;对于B,函数非奇非偶,不满足题意;对于C,f(-x)=-x|-x|=-x|x|=-f(x),是奇函数,又
 ,故是R上的增函数;对于D,函数是奇函数,但是增函数.
,故是R上的增函数;对于D,函数是奇函数,但是增函数.解答:由题意,对于A,函数是奇函数,但是减函数,故不满足题意;
对于B,函数非奇非偶,不满足题意;
对于C,f(-x)=-x|-x|=-x|x|=-f(x),是奇函数,又
 ,故是R上的增函数,故满足题意
,故是R上的增函数,故满足题意对于D,函数是奇函数,但是增函数,故不满足题意;
故选C.
点评:本题考查函数单调性与奇偶性的综合,解题的依据是函数单调性与奇偶性的定义.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
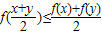 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数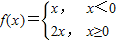
 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数