题目内容
设点P(m,n)是以y轴为对称轴,原点为顶点,焦点为(0,1)的抛物线C上的任意一点,过点P作抛物线的切线交抛物线的准线于点A(s,t).
(1)求抛物线C的标准方程;
(2)若m∈[1,4],求s的取值范围.
(1)求抛物线C的标准方程;
(2)若m∈[1,4],求s的取值范围.
分析:(1)由题意可得
=1,可得p=2,可得方程;(2)求导数可得切线斜率,可得切线方程和准线方程,可得s=
-
,可得s在[1,4]单调递增,进而可得答案.
| p |
| 2 |
| m |
| 2 |
| 2 |
| m |
解答: 解:(1)由题意可得
解:(1)由题意可得
=1,可得p=2,故可得方程为:x2=4y…(4分)
(2)过P(m,n)的切线斜率k=y′|x=m=
m.
∴切线方程为y-n=
m(x-m),准线方程为y=-1. …(8分)
∴-1-
m2=
ms-
m2.解得s=
-
. …(12分)
由函数的性质可得s在[1,4]单调递增,
∴smin=-
,smax=
.
∴s的取值范围是-
≤s≤
. …(15分)
 解:(1)由题意可得
解:(1)由题意可得| p |
| 2 |
(2)过P(m,n)的切线斜率k=y′|x=m=
| 1 |
| 2 |
∴切线方程为y-n=
| 1 |
| 2 |
∴-1-
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| m |
| 2 |
| 2 |
| m |
由函数的性质可得s在[1,4]单调递增,
∴smin=-
| 3 |
| 2 |
| 3 |
| 2 |
∴s的取值范围是-
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查抛物线的简单性质,涉及函数的单调性,属中档题.

练习册系列答案
相关题目
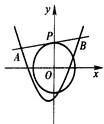 设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于A,B两点,点O是坐标原点.
设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于A,B两点,点O是坐标原点.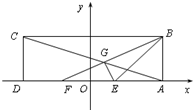 在矩形ABCD中,以DA所在直线为x轴,以DA中点O为坐标原点,建立如图所示的平面直角坐标系.已知点B的坐标为(3,2),E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为⊙H.
在矩形ABCD中,以DA所在直线为x轴,以DA中点O为坐标原点,建立如图所示的平面直角坐标系.已知点B的坐标为(3,2),E、F为AD的两个三等分点,AC和BF交于点G,△BEG的外接圆为⊙H.