Question

（2007•东城区一模）设函数f（x）=

2(x＞0) x2+bx+c(x≤0)

，若f（-4）=f（0），f（-2）=-2，则f（x）的解析式为f（x）=

f（x）=

2(x＞0) x2+4x+2(x≤0)

，关于x的方程f（x）=x的解的个数为

3

．

Answer 1

分析：利用待定系数法求解．先由x≤0时的解析式f（x）=x²+bx+c，再根据f（-4）=f（0），f（-2）=-2，列方程组即可解得f（x）的解析式．方程解的个数，就是函数y=f（x），y=x交点的个数，画出两个函数的图象即可得到本题的结论．

解答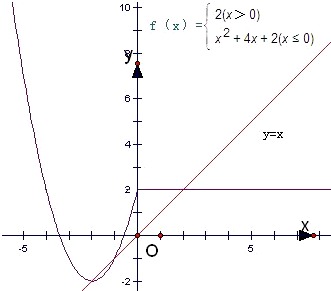：解：x≤0时的解析式f（x）=x²+bx+c，
则有：

16-4b+c=c 4-2b+c=-2

得：

b=4 c=2

∴函数f（x）的解析式为f（x）=

2(x＞0) x2+4x+2(x≤0)

．
关于x的方程：f（x）=x解的个数，就是函数y=f（x），y=x交点的个数，画出两个函数的图象如图：
由函数的图象可知，两个函数的图象有3个交点，所以方程有3个解；
故答案为：f（x）=

2(x＞0) x2+4x+2(x≤0)

；3．

点评：本题主要考查了根的存在性及根的个数判断，考查了函数的表示方法-解析式法，以及待定系数法，属于基础题．