题目内容
14.已知f(x)=(2x-3)n展开式的二项式系数和为64,且(2x-3)n=a0+a1(x-1)+a2(x-1)2+…+an(x-1)n.(1)求a2的值;(用数字作答)
(2)求|a0|+|a1|+|a2|+|a3|+…|an|的值.(用数字作答)
分析 (1)根据(2x-3)n展开式的二项式系数和求出n的值,化(2x-3)6=[-1+2(x-1)]6,求出a2的值;
(2)在(2x-3)6=[-1+2(x-1)]6=a0+a1(x-1)+a2(x-1)2+…+a9(x-1)6中,令x=0即可求出|a0|+|a1|+|a2|+|a3|+…|an|的值.
解答 解:(1)f(x)=(2x-3)n展开式的二项式系数和为64,
∴2n=64,解得n=6;
∵(2x-3)6=[-1+2(x-1)]6=a0+a1(x-1)+a2(x-1)2+…+a9(x-1)6,
∴a2=${C}_{6}^{2}$•(-1)4•22=60;
(2)在(2x-3)6=a0+a1(x-1)+a2(x-1)2+…+a6(x-1)6中,
即[-1+2(x-1)]6=a0+a1(x-1)+a2(x-1)2+…+a9(x-1)6,
令x=0,可得|a0|+|a1|+|a2|+|a3|+…|an|=(-1-2)6=729.
点评 本题考查了二项式定理以及二项展开式的通项公式应用问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知i是虚数单位,则(1+i)2的共轭复数是( )
| A. | -2i | B. | -2+i | C. | 2i | D. | 1+2i |
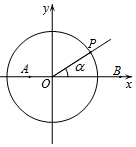 如图,在平面直角坐标系中,点$A(-\frac{1}{2},0)$,$B(\frac{3}{2},0)$,锐角α的终边与单位圆O交于点P.
如图,在平面直角坐标系中,点$A(-\frac{1}{2},0)$,$B(\frac{3}{2},0)$,锐角α的终边与单位圆O交于点P.