题目内容
已知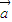
、
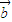均为非零向量，当
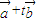（t∈R）的模取最小值时，①求t的值；
②已知
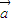与
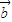为不共线向量，求证
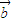与
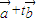垂直．
【答案】分析：（1）求出
的平方，展开化简，模取得最小值时，求出t的值．
（2）借助（1）直接求解（
）•
的值，推出值为0，即可说明
与
垂直．
解答：解：（1）（
）2=
=
2+t2
2+2t|
||
|cos＜
，
＞
=（t|
|+|
|cos＜
，
＞）2+|
|2（1-cos2＜
，
＞）
当t=
时．|
|有最小值
；
（2）
与
为不共线向量，由（1）可知此时，（
）•
=
+[
]|
|2=
-
=0
即（
）⊥
，夹角是90°．
点评：本题是中档题，考查向量的数量积的应用，考查计算能力，注意模的最小值的求法，存在关系的应用．
的平方，展开化简，模取得最小值时，求出t的值．（2）借助（1）直接求解（
）•
的值，推出值为0，即可说明
与
垂直．解答：解：（1）（
）2=
=
2+t2
2+2t|
||
|cos＜
，
＞=（t|
|+|
|cos＜
，
＞）2+|
|2（1-cos2＜
，
＞）当t=
时．|
|有最小值
；（2）
与
为不共线向量，由（1）可知此时，（
）•
=
+[
]|
|2=
-
=0即（
）⊥
，夹角是90°．点评：本题是中档题，考查向量的数量积的应用，考查计算能力，注意模的最小值的求法，存在关系的应用．
练习册系列答案
名校课堂系列答案
相关题目
、
均为非零向量，命题p：
＞0，命题q：
，
均为非零向量，
，
与
与
成立的( )
．必要不充分条件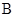 
．充分不必要条件
．充分必要条件 
．既不充分也不必要条件
、
均为非零向量，命题p：
＞0，命题q：
与
的夹角为锐角，则p是q成立的（ ）
、
均为非零向量，命题p：
＞0，命题q：
与
的夹角为锐角，则p是q成立的（ ）