题目内容
若下列方程: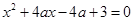 ,
,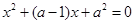 ,
,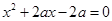 ,至少有一个方程有实根,试求实数
,至少有一个方程有实根,试求实数 的取值范围.
的取值范围.
解:设三个方程均无实根,则有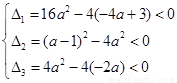
解得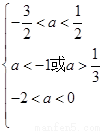 ,即
,即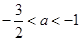 .
.
所以当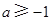 或
或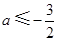 时,三个方程至少有一个方程有实根.
时,三个方程至少有一个方程有实根.
【答案】
 或
或 时,三个方程至少有一个方程有实根.
时,三个方程至少有一个方程有实根.
【解析】
试题分析:设三个方程均无实根,则有
解得 ,即
,即 .
.
所以当 或
或 时,三个方程至少有一个方程有实根.
时,三个方程至少有一个方程有实根.
考点:本题主要考查方程根的讨论,不等式组的解法。
点评:典型题,本解法很好地体现了“正难则反”的解题策略,简化了解题过程。

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 的离心率e=
的离心率e= ,则b=c(c为半焦距).
,则b=c(c为半焦距). 的焦点到渐近线的距离为b.
的焦点到渐近线的距离为b. 的离心率e=
的离心率e= ,则b=c(c为半焦距).
,则b=c(c为半焦距). 的焦点到渐近线的距离为b.
的焦点到渐近线的距离为b.