利用函数的单调性定义证明函数f(x)=ax2+bx+c在区间(-∞,-)上是减函数. 题目和参考答案——青夏教育精英家教网—

题目内容

利用函数的单调性定义证明函数f(x)=ax²＋bx+c(a＞0)在区间(-∞,-)上是减函数.

试题答案

相关练习册答案

思路解析:证明的关键是作差后分解因式,并正确地利用区间(-∞,-］确定其符号.

证明:在(-∞,-］上任意选取x₁,x₂,且x₁＜x₂,

则f(x₁)=ax₁²+bx₁+c,f(x₂)=ax₂²+bx₂+c.

∴f(x₁)-f(x₂)=ax₁²+bx₁+c-(ax₂²+bx₂+c)=a(x₁²-x₂²)+b(x₁-x₂)=(x₁-x₂)［a(x₁+x₂)+b］=a(x₁-x₂)［(x₁+x₂)+］.

∵-∞＜x₁＜x₂≤-,

∴x₁-x₂＜0,-∞＜x₁+x₂＜-.

∴x₁+x₂+＜0.

又∵a＞0,∴a(x₁-x₂)［(x₁+x₂)+ ］＞0,即f(x₁)＞f(x₂).

∴函数f(x)=ax²+bx+c(a＞0)在区间(-∞,- )上是减函数.

深化升华

在利用函数单调性的定量化定义证明函数的单调性时,要特别注意所给区间在证明过程中所发挥的作用.对于同一个函数所给区间的不同则可能有不同的单调性.甚至没有单调性.在例题2中正因为利用了-∞＜x₁＜x₂≤-,才说明了x₁+x₂+的符号,进而说明了a(x₁-x₂)［(x₁+x₂)+ ］的符号.

练习册系列答案

课堂点睛系列答案

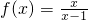利用函数的单调性定义证明函 $数学公式$ ，x∈[2，4]是单调递减函数，并求函数的值域．