题目内容
已知函数f(x)=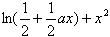 -ax(a为常数,a>0)。
-ax(a为常数,a>0)。
(1)若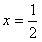 是函数f(x)的一个极值点,求a的值;
是函数f(x)的一个极值点,求a的值;
(2)求证:当0<a≤2时,f(x)在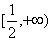 上是增函数;
上是增函数;
(3)若对任意的a∈(1,2),总存在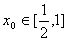 ,使不等式f(x0)>m(1-a2)成立,求实数m的取值范围。
,使不等式f(x0)>m(1-a2)成立,求实数m的取值范围。
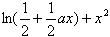 -ax(a为常数,a>0)。
-ax(a为常数,a>0)。(1)若
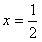 是函数f(x)的一个极值点,求a的值;
是函数f(x)的一个极值点,求a的值;(2)求证:当0<a≤2时,f(x)在
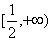 上是增函数;
上是增函数;(3)若对任意的a∈(1,2),总存在
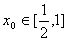 ,使不等式f(x0)>m(1-a2)成立,求实数m的取值范围。
,使不等式f(x0)>m(1-a2)成立,求实数m的取值范围。解: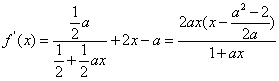
(1)由已知,得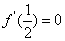 且
且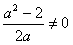
∴a2-a-2=0
∵a>0
∴a=2。
(2)当0<a≤2时,∵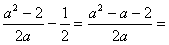
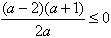
∴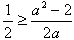
∴当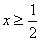 时,
时,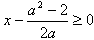
又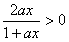
∴f′(x)≥0,
故 f(x)在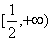 上是增函数。
上是增函数。
(3)a∈(1,2)时,由(2)知,f(x)在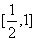 上的最大值为
上的最大值为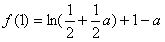
于是问题等价于:对任意的a∈(1,2),不等式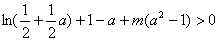 恒成立
恒成立
记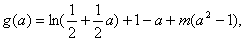 (1<a<2)
(1<a<2)
则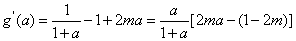
当m=0时,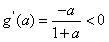
∴g(a)在区间(1,2)上递减,
此时,g(a)<g(1)=0,
∵a2-1>0,
∴m≤0时不可能使g(a)>0恒成立,故必有m>0
∴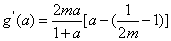
若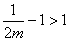 ,可知g(a)在区间
,可知g(a)在区间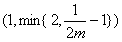 上递减,
上递减,
在此区间上,有g(a)<g(1)=0,与g(a)>0恒成立矛盾,
故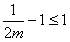 ,
,
这时,g′(a)>0,g(a)在(1,2)上递增,恒有g(a)>g(1)=0,满足题设要求,
∴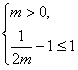 ,即
,即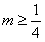 ,
,
所以,实数m的取值范围为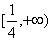 。
。
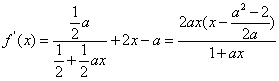
(1)由已知,得
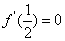 且
且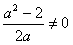
∴a2-a-2=0
∵a>0
∴a=2。
(2)当0<a≤2时,∵
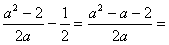
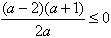
∴
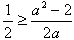
∴当
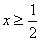 时,
时,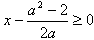
又
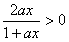
∴f′(x)≥0,
故 f(x)在
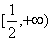 上是增函数。
上是增函数。(3)a∈(1,2)时,由(2)知,f(x)在
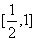 上的最大值为
上的最大值为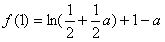
于是问题等价于:对任意的a∈(1,2),不等式
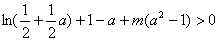 恒成立
恒成立记
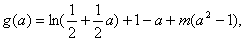 (1<a<2)
(1<a<2)则
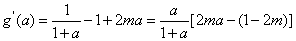
当m=0时,
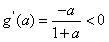
∴g(a)在区间(1,2)上递减,
此时,g(a)<g(1)=0,
∵a2-1>0,
∴m≤0时不可能使g(a)>0恒成立,故必有m>0
∴
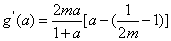
若
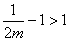 ,可知g(a)在区间
,可知g(a)在区间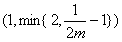 上递减,
上递减,在此区间上,有g(a)<g(1)=0,与g(a)>0恒成立矛盾,
故
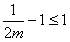 ,
,这时,g′(a)>0,g(a)在(1,2)上递增,恒有g(a)>g(1)=0,满足题设要求,
∴
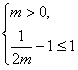 ,即
,即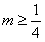 ,
,所以,实数m的取值范围为
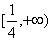 。
。
练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|