题目内容
 如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且KF=
如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且KF=| 1 | 2 |
(Ⅰ)求证:BF∥平面ACE;
(Ⅱ)求证:平面AFC⊥平面EFC.
分析:(Ⅰ)记AC与BD的交点为O,则DO=BO=
BD,连接EO,则可证出四边形EFBO是平行四边形,从而BF∥EO,最后结合线面平行的判定定理,可得BF∥平面ACE;
(II)连接FO,在平行四边形EFOD中,根据ED∥FO结合ED⊥平面ABCD,得FO⊥平面ABCD,所以BD⊥FO,结合ABCD为正方形,可得BD⊥平面AFC.所以BD的平行线EF⊥平面AFC,最后根据面面垂直的判定定理,可得平面AFC⊥平面EFC.
| 1 |
| 2 |
(II)连接FO,在平行四边形EFOD中,根据ED∥FO结合ED⊥平面ABCD,得FO⊥平面ABCD,所以BD⊥FO,结合ABCD为正方形,可得BD⊥平面AFC.所以BD的平行线EF⊥平面AFC,最后根据面面垂直的判定定理,可得平面AFC⊥平面EFC.
解答:解:(Ⅰ)记AC与BD的交点为O,则DO=BO=
BD,连接EO,(1分)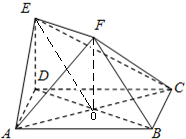
∵EF∥BD且EF=
BD,
∴EF∥BO且EF=BO,则四边形EFBO是平行四边形,(2分)
∴BF∥EO,
又∵EO?面ACE,BF?面ACE,
∴BF∥平面ACE; (4分)
(Ⅱ)连接FO,
∵EF∥BD且EF=
BD,
∴EF∥BO且EF=BO,则四边形EFOD是平行四边形.(6分)
∴ED∥FO,
∵ED⊥平面ABCD,
∴FO⊥平面ABCD(8分)
又∵BD?平面ABCD
∴BD⊥FO,
∵BD⊥AC,AC∩FO=O,AC、FO?平面AFC
∴BD⊥平面AFC(10分)
∵EF∥BD,∴EF⊥平面AFC,
∵EF?平面AFC,∴平面AFC⊥平面EFC. (12分)
| 1 |
| 2 |

∵EF∥BD且EF=
| 1 |
| 2 |
∴EF∥BO且EF=BO,则四边形EFBO是平行四边形,(2分)
∴BF∥EO,
又∵EO?面ACE,BF?面ACE,
∴BF∥平面ACE; (4分)
(Ⅱ)连接FO,
∵EF∥BD且EF=
| 1 |
| 2 |
∴EF∥BO且EF=BO,则四边形EFOD是平行四边形.(6分)
∴ED∥FO,
∵ED⊥平面ABCD,
∴FO⊥平面ABCD(8分)
又∵BD?平面ABCD
∴BD⊥FO,
∵BD⊥AC,AC∩FO=O,AC、FO?平面AFC
∴BD⊥平面AFC(10分)
∵EF∥BD,∴EF⊥平面AFC,
∵EF?平面AFC,∴平面AFC⊥平面EFC. (12分)
点评:本题以一个特殊多面体为例,要我们证明线面平行和面面垂直,着重考查了线面平行的判定定理和面面垂直的判定理等知识,属于中档题.

练习册系列答案
相关题目
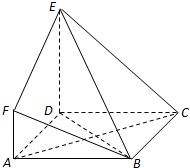 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°. 如图,ABCD是边长为a的菱形,且∠BAD=60°,△PAD为正三角形,且面PAD⊥面ABCD.
如图,ABCD是边长为a的菱形,且∠BAD=60°,△PAD为正三角形,且面PAD⊥面ABCD. 如图,ABCD是边长为2的正方形,面EAD⊥面ABCD,且EA=ED,EF∥AB,且EF=1,O是线段AD的中点,三棱锥F-OBC的体积为
如图,ABCD是边长为2的正方形,面EAD⊥面ABCD,且EA=ED,EF∥AB,且EF=1,O是线段AD的中点,三棱锥F-OBC的体积为 (2012•宁城县模拟)如图,ABCD是边长为1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF.
(2012•宁城县模拟)如图,ABCD是边长为1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF. 如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):
如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕将正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B';折痕与AB交于点E,以EB和EB’为邻边作平行四边形EB’MB.若以B为原点,BC所在直线为x轴建立直角坐标系(如下图):