题目内容
设θ∈[0,
解析:sin2θ+2mcosθ-m+1<0![]() cos2θ-2mcosθ+m-2>0.
cos2θ-2mcosθ+m-2>0.
令y=cos2θ-2mcosθ+m-2
=(cosθ-m)2-m2+m-2.
要使不等式恒成立,即需要y>0恒成立.
当m≥1,cosθ=1时,ymin=(1-m)2-m2+m-2=-m-1>0,则m<-1(舍).
当m≤-1,cosθ=-1时,ymin=(-1-m)2-m2+m-2=3m-1>0,则m>![]() (舍).
(舍).
当-1<m<1,cosθ=m时,ymin=-m2+m-2>0,m不存在.
综上可知,不存在这样的m,使得原不等式恒成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
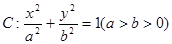 的离心率为
的离心率为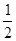 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线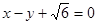 相切.
相切.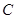 的方程;
的方程;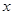 轴对称的任意两个不同的点,连接
轴对称的任意两个不同的点,连接 交椭圆
交椭圆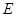 ,证明直线
,证明直线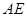 与
与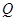 ;
;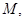
 两点,求
两点,求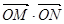 的取值范围.
的取值范围.