题目内容
已知向量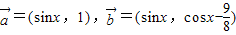 ,设函数
,设函数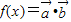 ,x∈[0,π]
,x∈[0,π](1)求f(x)的单调区间;
(2)若f(x)=0在区间[0,π]上有两个不同的根α,β,求cos(α+β)的值.
【答案】分析:(1)由题意,可先由向量的数量积运算及三角恒等变换,得出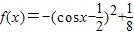 ,由此函数是一个复合函数,分类讨论cosx的取值范围,利用复合函数的单调性的判断规则判断出单调性区间;
,由此函数是一个复合函数,分类讨论cosx的取值范围,利用复合函数的单调性的判断规则判断出单调性区间;
(2)法一:f(x)=0在区间[0,π]上有两个不同的根α,β,可得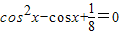 有两个根,此两根为cosα,cosβ,由根与系数的关系
有两个根,此两根为cosα,cosβ,由根与系数的关系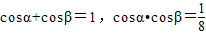 ,再由由到角三角函数关系,解出
,再由由到角三角函数关系,解出 易求cos(α+β)的值;
易求cos(α+β)的值;
法二:f(x)=0在区间[0,π]上有两个不同的根α,β,可得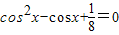 有两个根,此两根为cosα,cosβ,解一元二次方程
有两个根,此两根为cosα,cosβ,解一元二次方程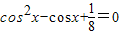 可得出cosα,cosβ的值,再解出两角的正弦值,代入cos(α+β)的展开式,即可求cos(α+β)的值
可得出cosα,cosβ的值,再解出两角的正弦值,代入cos(α+β)的展开式,即可求cos(α+β)的值
解答:解:(1)∵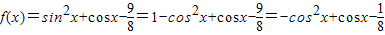
∴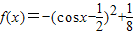
令t=cosx,
当 时,
时, ,且t=cosx为减函数
,且t=cosx为减函数
又 在
在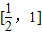 上时减函数,
上时减函数,
∴f(x)在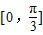 上是增函数
上是增函数
当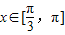 时,
时,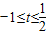 ,且t=cosx为减函数
,且t=cosx为减函数
又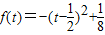 在
在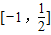 上时增函数,
上时增函数,
∴f(x)在 上是减函数
上是减函数
综上,f(x)的单调区间为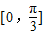 ,
,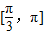
(2)法一:由f(x)=0得,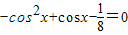 ,即
,即
令t=cosx,则cosα,cosβ是方程 的两个根,从而
的两个根,从而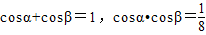
sin2α•sin2β=(1-cos2α)(1-cos2β)=1-(cos2α+cos2β)+cos2α•cos2β=
∴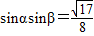 ,
,
∴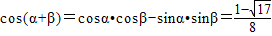
法二:由f(x)=0得,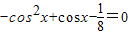 ,即
,即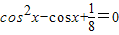
不妨设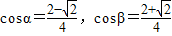 ,
,
则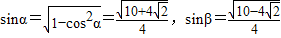 ,
,
∴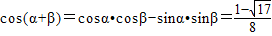
点评:本题考查平面向量与三角函数的综合题,考查了平面向量的数量积公式,三角函数的复合函数单调性判断,解三角方程,两角和与差的余弦函数,解题的关键是熟练掌握数量积公式及三角恒等变换公式,一元二次方程的解法,根与系数的关系等知训,本题的难点是第一问中对函数单调敬意的求解,由于本题的函数是内层为单调性函数,外层函数不是单调性函数,解题时由外而内,根据外层函数的单调区间确定出内层函数的相应单调区间即可得出复合函数的单调区间,题后注意总结这类题的解题的规律,本题运算量大,综合性强,考查了推理判断的能力及计算能力,分类讨论的思想,方程的思想
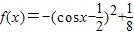 ,由此函数是一个复合函数,分类讨论cosx的取值范围,利用复合函数的单调性的判断规则判断出单调性区间;
,由此函数是一个复合函数,分类讨论cosx的取值范围,利用复合函数的单调性的判断规则判断出单调性区间;(2)法一:f(x)=0在区间[0,π]上有两个不同的根α,β,可得
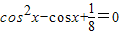 有两个根,此两根为cosα,cosβ,由根与系数的关系
有两个根,此两根为cosα,cosβ,由根与系数的关系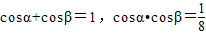 ,再由由到角三角函数关系,解出
,再由由到角三角函数关系,解出 易求cos(α+β)的值;
易求cos(α+β)的值;法二:f(x)=0在区间[0,π]上有两个不同的根α,β,可得
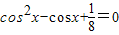 有两个根,此两根为cosα,cosβ,解一元二次方程
有两个根,此两根为cosα,cosβ,解一元二次方程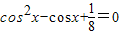 可得出cosα,cosβ的值,再解出两角的正弦值,代入cos(α+β)的展开式,即可求cos(α+β)的值
可得出cosα,cosβ的值,再解出两角的正弦值,代入cos(α+β)的展开式,即可求cos(α+β)的值解答:解:(1)∵
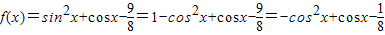
∴
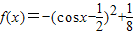
令t=cosx,
当
 时,
时, ,且t=cosx为减函数
,且t=cosx为减函数又
 在
在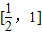 上时减函数,
上时减函数,∴f(x)在
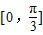 上是增函数
上是增函数当
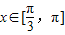 时,
时,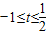 ,且t=cosx为减函数
,且t=cosx为减函数又
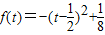 在
在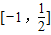 上时增函数,
上时增函数,∴f(x)在
 上是减函数
上是减函数综上,f(x)的单调区间为
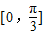 ,
,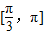
(2)法一:由f(x)=0得,
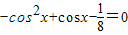 ,即
,即
令t=cosx,则cosα,cosβ是方程
 的两个根,从而
的两个根,从而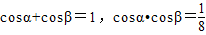
sin2α•sin2β=(1-cos2α)(1-cos2β)=1-(cos2α+cos2β)+cos2α•cos2β=

∴
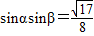 ,
,∴
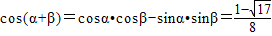
法二:由f(x)=0得,
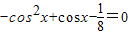 ,即
,即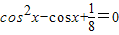
不妨设
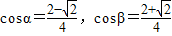 ,
,则
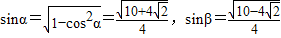 ,
,∴
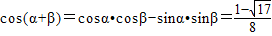
点评:本题考查平面向量与三角函数的综合题,考查了平面向量的数量积公式,三角函数的复合函数单调性判断,解三角方程,两角和与差的余弦函数,解题的关键是熟练掌握数量积公式及三角恒等变换公式,一元二次方程的解法,根与系数的关系等知训,本题的难点是第一问中对函数单调敬意的求解,由于本题的函数是内层为单调性函数,外层函数不是单调性函数,解题时由外而内,根据外层函数的单调区间确定出内层函数的相应单调区间即可得出复合函数的单调区间,题后注意总结这类题的解题的规律,本题运算量大,综合性强,考查了推理判断的能力及计算能力,分类讨论的思想,方程的思想

练习册系列答案
相关题目
 ,设函数
,设函数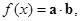 其中xÎR.
其中xÎR. 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.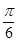 个单位得到
个单位得到 的图象,求
的图象,求 ,设函数f(x)=m·n-1,
,设函数f(x)=m·n-1,  ,求
,求 的值.
的值.