Question

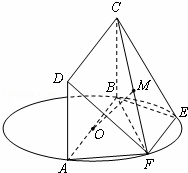
如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．

（1）求证：AF⊥平面CBF；

（2）设FC的中点为M，求证：OM∥平面DAF；

（3）设平面CBF将几何体EFABCD分成的两个锥体的体积分别为V_F﹣ABCD，V_F﹣CBE，求V_F﹣ABCD：V_F﹣CBE．

Answer 1

考点：

空间中直线与平面之间的位置关系．

专题：

综合题；转化思想．

分析：

（1）可以先由平面ABCD⊥平面ABEF以及CB⊥AB证得CB⊥平面ABEF，⇒AF⊥CB．又因为AB为圆O的直径⇒AF⊥BF，就可证：AF⊥平面CBF；

（2）取DF的中点为N，利用MNAO⇒MNAO为平行四边形⇒OM∥AN即可．既用线线平行来证线面平行．

（3）先把两个锥体的体积套公式求出来，就可求出其体积之比．

解答：

解：（1）证明：由平面ABCD⊥平面ABEF，CB⊥AB，

平面ABCD∩平面ABEF=AB，

得CB⊥平面ABEF，

而AF⊂平面ABEF，所以AF⊥CB（2分）

又因为AB为圆O的直径，

所以AF⊥BF，（3分）

又BF∩CB=B，所以AF⊥平面CBF（4分）

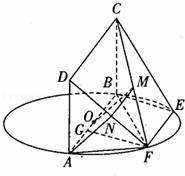
（2）证明：设DF的中点为N，连接AN，MN

则MNCD，又AOCD

则MNAO，所以四边形MNAO为平行四边形，（6分）

所以OM∥AN，又AN⊂平面DAF，OM⊄平面DAF，

所以OM∥平面DAF．（8分）

（3）过点F作FG⊥AB于G，因为平面ABCD⊥平面ABEF，

所以FG⊥平面ABCD，所以（9分）

因为CB⊥平面ABEF，

所以（11分）

所以V_F﹣ABCD：V_F﹣CBE=4：1．（12分）

点评：

本题是对立体几何知识的综合考查，涉及到线面垂直，线面平行和棱锥体积公式．是道综合性极强的好题．在证明线面平行时，其常用方法是在平面内找已知直线平行的直线．当然也可以用面面平行来推导线面平行．