题目内容
设函数![]() ,A0为坐标原点,An为函数y=f(x)图象上横坐标为n(n∈N*)的点,向量
,A0为坐标原点,An为函数y=f(x)图象上横坐标为n(n∈N*)的点,向量![]() ,向量i=(1,0),设θn为向量an与向量i的夹角,则满足
,向量i=(1,0),设θn为向量an与向量i的夹角,则满足![]() 的最大整数n是 .
的最大整数n是 .
| 考点: | 两角和与差的正切函数. |
| 专题: | 压轴题. |
| 分析: | 先确定点An=(n,f(n)),再确定 |
| 解答: | 解:由题意知An=(n,f(n)), 则θn为直线A0An的倾斜角,所以tanθn= 所以tanθ1= 则有 故满足要求的最大整数n是3. |
| 点评: | 本题综合考查向量的夹角与运算及正切函数的定义与求值. |

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
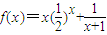 ,A为坐标原点,An为函数y=f(x)图象上横坐标为n(n∈N*)的点,向量
,A为坐标原点,An为函数y=f(x)图象上横坐标为n(n∈N*)的点,向量 ,向量i=(1,0),设θn为向量an与向量i的夹角,则满足
,向量i=(1,0),设θn为向量an与向量i的夹角,则满足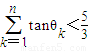 的最大整数n是 .
的最大整数n是 .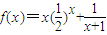 ,A为坐标原点,An为函数y=f(x)图象上横坐标为n(n∈N*)的点,向量
,A为坐标原点,An为函数y=f(x)图象上横坐标为n(n∈N*)的点,向量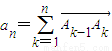 ,向量i=(1,0),设θn为向量an与向量i的夹角,则满足
,向量i=(1,0),设θn为向量an与向量i的夹角,则满足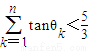 的最大整数n是 .
的最大整数n是 .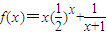 ,A为坐标原点,An为函数y=f(x)图象上横坐标为n(n∈N*)的点,向量
,A为坐标原点,An为函数y=f(x)图象上横坐标为n(n∈N*)的点,向量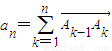 ,向量i=(1,0),设θn为向量an与向量i的夹角,则满足
,向量i=(1,0),设θn为向量an与向量i的夹角,则满足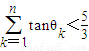 的最大整数n是 .
的最大整数n是 . ,A为坐标原点,An为函数y=f(x)图象上横坐标为n(n∈N*)的点,向量
,A为坐标原点,An为函数y=f(x)图象上横坐标为n(n∈N*)的点,向量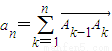 ,向量i=(1,0),设θn为向量an与向量i的夹角,则满足
,向量i=(1,0),设θn为向量an与向量i的夹角,则满足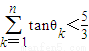 的最大整数n是 .
的最大整数n是 .