题目内容
(12分)由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下: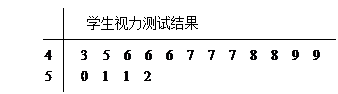

(Ⅰ)指出这组数据的众数和中位数;
(Ⅱ)若视力测试结果不低丁5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(Ⅲ)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记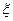 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求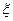 的分布列及数学期望.
的分布列及数学期望.
(Ⅰ)众数:4.6和4.7;中位数:4.75
(Ⅱ)
(Ⅲ)分布列为










 .
.
另解: ,
, =
=
解析

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(2) 试预测加工10个零件需要多少时间?

(本小题满分12分)高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
 | ① | ② |
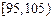 | | 0.050 |
 | | 0.200 |
 | 12 | 0.300 |
 | | 0.275 |
 | 4 | ③ |
 | | 0.050 |
| 合 计 | | ④ |
 、③、④处的数值分别是多少?
、③、④处的数值分别是多少?(2)在坐标系中画出
 的频率分布直方图;
的频率分布直方图;(3)根据题中信息估计总体平均数,并估计总体落在
 中的概率。
中的概率。 (10分)为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量。产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95),由此得到频率分布直方图,如右图。
(1)请填完整表格;
(2)估算众数,中位数,平均数。
| 分组 | 45~55 | 55~65 | 65~75 | 75~85 | 85~95 |
| 频数 | | | | | |
| 频率 | | | | | |

假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
 | 2 | 3 | 4 | 5 | 6 |
 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,求出y关于x的线性回归方程
 ;
;(Ⅲ)估计使用年限为10年时,维修费用约是多少?
(
 )
) 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2) 请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
 ;
;(3) 已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考数据: 3×2.5+4×3+5×4+6×4.5=66.5)
某农场种植火龙果的成本x(单位:万元)与收益y(单位:万元)之间关系如下:
| x | 2 | 4 | 6 | 8 | 10 |
| Y | 10 | 13 | 15 | 18 | 20 |
(2)若收益不少于16万元,则投入的成本不少于多少万元。
(提示:

 )
)
(本小题满分14分)为了检测某条生产线上产品的尺寸。现从该条生产线上每隔一定时间取一件产品,共取了50件,测得其产品尺寸后,画得其频率分布直方图如下。
|
 (1)分别求尺寸在[10,15)和[20,25)内产品的频率。
(1)分别求尺寸在[10,15)和[20,25)内产品的频率。(2)求尺寸在
 内产品的个数.
内产品的个数. 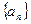 的前四项,后6组的频数从左到右依次是等差数列
的前四项,后6组的频数从左到右依次是等差数列 的前六项.
的前六项. 若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率
若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率 的大小.
的大小.