题目内容
定义在R上的函数f(x)=ax3+bx2+cx(a≠0)的单调增区间为(-1,1),若方程3a(f(x))2+2bf(x)+c=0恰有4个不同的实根,则实数a的值为.( )
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
分析:根据函数的单调区间求出a,b,c的关系,然后利用导数研究三次函数的极值,利用数形结合即可得到a的结论.
解答:解:∵函数f(x)=ax3+bx2+cx(a≠0)的单调增区间为(-1,1),
∴f'(x)>0的解集为(-1,1),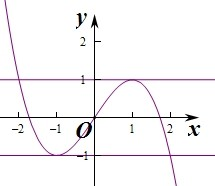
即f'(x)=3ax2+2bx+c>0的解集为(-1,1),
∴a<0,且x=-1和x=1是方程f'(x)=3ax2+2bx+c=0的两个根,
即-1+1=-
=0,-1×1=
=-1,
解得b=0,c=-3a.
∴f(x)=ax3+bx2+cx=ax3-3ax=ax(x2-3),
则方程3a(f(x))2+2bf(x)+c=0等价为3a(f(x))2-3a=0,
即(f(x))2=1,即f(x)=±1.
要使方程3a(f(x))2+2bf(x)+c=0恰有4个不同的实根,即f(x)=±1.各有2个不同的根,
即函数f(x)的极值等于±1,
∵f(x)=ax3+bx2+cx=ax3-3ax=ax(x2-3),
∴f'(x)=3ax2-3a=3a(x2-1),
∵a<0,
∴当f'(x)>0得-1<x<1,此时函数单调递增,
当f'(x)<0得x<-1或x>1,此时函数单调递减,
∴当x=1时,函数取得极大值f(1)=-2a,
当x=-1时,函数取得极小值f(-1)=2a,
由f(1)=-2a=1且f(-1)=2a=-1得,a=-
,
故选:B.
∴f'(x)>0的解集为(-1,1),

即f'(x)=3ax2+2bx+c>0的解集为(-1,1),
∴a<0,且x=-1和x=1是方程f'(x)=3ax2+2bx+c=0的两个根,
即-1+1=-
| 2b |
| 3a |
| c |
| 3a |
解得b=0,c=-3a.
∴f(x)=ax3+bx2+cx=ax3-3ax=ax(x2-3),
则方程3a(f(x))2+2bf(x)+c=0等价为3a(f(x))2-3a=0,
即(f(x))2=1,即f(x)=±1.
要使方程3a(f(x))2+2bf(x)+c=0恰有4个不同的实根,即f(x)=±1.各有2个不同的根,
即函数f(x)的极值等于±1,
∵f(x)=ax3+bx2+cx=ax3-3ax=ax(x2-3),
∴f'(x)=3ax2-3a=3a(x2-1),
∵a<0,
∴当f'(x)>0得-1<x<1,此时函数单调递增,
当f'(x)<0得x<-1或x>1,此时函数单调递减,
∴当x=1时,函数取得极大值f(1)=-2a,
当x=-1时,函数取得极小值f(-1)=2a,
由f(1)=-2a=1且f(-1)=2a=-1得,a=-
| 1 |
| 2 |
故选:B.
点评:本题主要考查方程根的个数的应用,利用方程和函数之间的关系,作出函数的图象,利用数形结合是解决本题的关键.利用导数研究函数的极值是解决本题的突破点.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目