题目内容
已知F为双曲线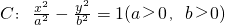 的右焦点,P为双曲线C右支上一点,且位于x轴上方,M为直线
的右焦点,P为双曲线C右支上一点,且位于x轴上方,M为直线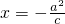 上一点,O为坐标原点,已知
上一点,O为坐标原点,已知 ,且
,且 ,则双曲线C的离心率为
,则双曲线C的离心率为
- A.2
- B.

- C.

- D.4
A
分析:先确定M的坐标,再确定P的坐标,代入双曲线方程,即可求得结论.
解答:由题意,M位于x轴上方
∵ ,M为直线
,M为直线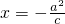 上一点
上一点
∴M( ,
, )
)
∵
∴四边形OMPF为菱形
∴P(c ,
, ),即
),即
代入双曲线方程可得
化简可得c2=4a2
∴c=2a,
∴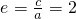
故选A.
点评:本题考查双曲线的性质,考查向量知识的运用,考查学生的计算能力,属于中档题.
分析:先确定M的坐标,再确定P的坐标,代入双曲线方程,即可求得结论.
解答:由题意,M位于x轴上方
∵
 ,M为直线
,M为直线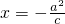 上一点
上一点∴M(
 ,
, )
)∵

∴四边形OMPF为菱形
∴P(c
 ,
, ),即
),即
代入双曲线方程可得

化简可得c2=4a2
∴c=2a,
∴
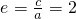
故选A.
点评:本题考查双曲线的性质,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目