题目内容
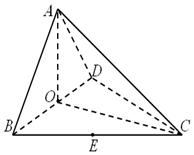
(本小题满分14分)如图,在四面体A?BCD中,AD^平面BCD,BC^CD,AD=2,BD=2.M是AD的中点.
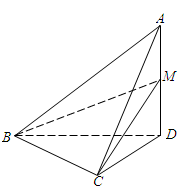
(1)证明:平面ABC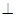 平面ADC;
平面ADC;
(2)若ÐBDC=60°,求二面角C?BM?D的大小.

(1)证明:平面ABC
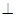 平面ADC;
平面ADC;(2)若ÐBDC=60°,求二面角C?BM?D的大小.
(1)见解析(2)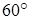
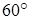
试题分析:(1)证明面面垂直几何法就要证线面垂直,要证线面垂直就要证线线垂直;线线、线面、面面垂直之间相互转化. 由题意知从点
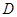 出发的三条件直线两两垂直,从而
出发的三条件直线两两垂直,从而 ,又
,又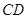 在平面
在平面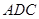 内,所以可证得平面ABC
内,所以可证得平面ABC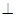 平面ADC.证明面面垂直向量法可证法向量垂直,由题意知从点
平面ADC.证明面面垂直向量法可证法向量垂直,由题意知从点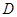 出发的三条件直线两两垂直,可以建立空间直角坐标系.
出发的三条件直线两两垂直,可以建立空间直角坐标系.(2)求二面角可用两种向量法(面向量和法向量)或几何法,面向量法即在两个半平面内分别从顶点
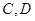 出发与棱
出发与棱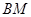 垂直的两个向量所成的角.几何法(三垂线法)重点是找到二面角的平面角,①在几何体内找第三个平面与二面角的两个半平都垂直,交线所成角即为平面角;如果找不到可以退而求其次,找第三个平面与二面角的其中一个半平垂直
垂直的两个向量所成的角.几何法(三垂线法)重点是找到二面角的平面角,①在几何体内找第三个平面与二面角的两个半平都垂直,交线所成角即为平面角;如果找不到可以退而求其次,找第三个平面与二面角的其中一个半平垂直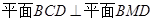 .②
.②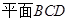 与另外一个半
与另外一个半 交于点
交于点 ,过点
,过点 作交线
作交线 的垂线
的垂线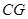 ③过点
③过点 作棱
作棱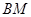 的垂线
的垂线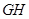 ④连
④连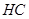 所得到的
所得到的 为二面角的平面角⑤在直角三角形
为二面角的平面角⑤在直角三角形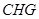 求角.用法向量法求二面角不容易判断所求出的是二面角还是其补角,所以尽量不用它.
求角.用法向量法求二面角不容易判断所求出的是二面角还是其补角,所以尽量不用它.试题解析:
(1)

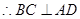
又

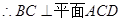 (4分)
(4分)又
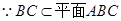
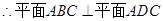 (6分)
(6分)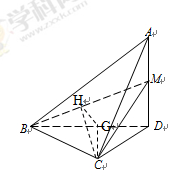
(2)作CG^BD于点G,作GH^BM于点HG,连接CH. (8分)

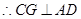
又
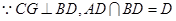
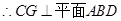
又
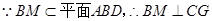
又
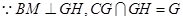
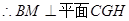

所以ÐCHG为二面角的平面角. (10分)
在Rt△BCD中,
CD=BD
 =
=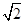 ,CG=CD
,CG=CD ,BG=BC
,BG=BC
在Rt△BDM中,HG=
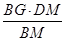 =
=
在Rt△CHG中,tanÐCHG=
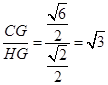
所以
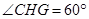 即二面角C-BM-D的大小为60°. (14分)
即二面角C-BM-D的大小为60°. (14分)
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
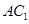 ∥平面
∥平面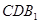 ;
;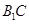 所成角的余弦值.
所成角的余弦值.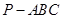 中,
中,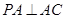 ,
,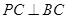 ,
,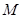 为
为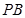 的中点,
的中点,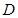 为
为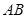 的中点,且
的中点,且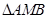 为正三角形.
为正三角形.
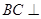 平面
平面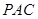 ;
;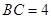 ,
,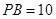 ,求点
,求点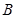 到平面
到平面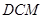 的距离.
的距离.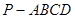 中,底面为直角梯形,
中,底面为直角梯形,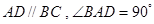 ,
,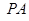 垂直于底面
垂直于底面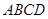 ,
,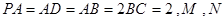 分别为
分别为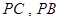 的中点.
的中点.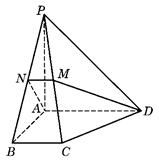
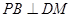 ;
; 到平面
到平面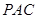 的距离.
的距离.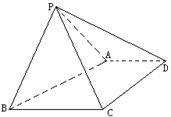
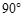 ,且AB=2AD=2DC=2PD=4,E为PA的中点.
,且AB=2AD=2DC=2PD=4,E为PA的中点.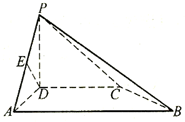
 中,
中,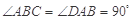 ,
,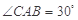 ,
,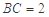 ,
,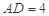 . 把
. 把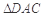 沿对角线
沿对角线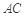 折起到
折起到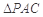 的位置,如图2所示,使得点
的位置,如图2所示,使得点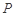 在平面
在平面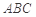 上的正投影
上的正投影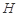 恰好落在线段
恰好落在线段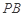 ,点
,点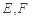 分别为线段
分别为线段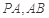 的中点.
的中点. 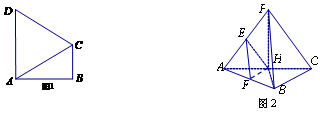
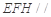 平面
平面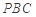 ;
;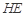 与平面
与平面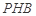 所成角的正弦值;
所成角的正弦值;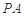 上是否存在一点
上是否存在一点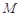 ,使得
,使得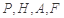 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.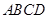 中,
中,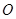 、
、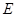 分别是
分别是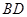 、
、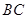 的中点,
的中点,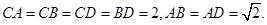
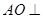 平面
平面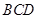 ;
;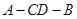 的正切值;
的正切值;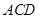 的距离.
的距离.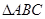 中,
中,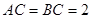 ,
,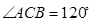 ,
,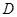 为
为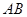 的中点,
的中点,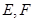 分别在线段
分别在线段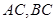 上的动点,且
上的动点,且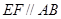 ,
,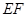 交
交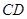 于
于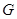 ,把
,把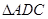 沿
沿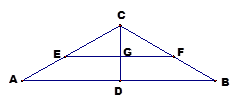
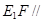 平面
平面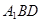 ;
;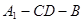 为直二面角时,是否存在点
为直二面角时,是否存在点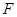 ,使得直线
,使得直线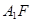 与平面
与平面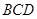 所成的角为
所成的角为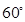 ,若存在求
,若存在求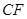 的长,若不存在说明理由。
的长,若不存在说明理由。