题目内容
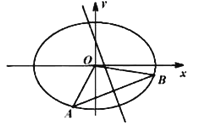
【题目】已知![]() 、
、![]() 为椭圆
为椭圆![]() (
(![]() )和双曲线
)和双曲线![]() 的公共顶点,
的公共顶点,![]() 、
、![]() 分为双曲线和椭圆上不同于
分为双曲线和椭圆上不同于![]() 、
、![]() 的动点,且满足
的动点,且满足![]() ,设直线
,设直线![]() 、
、![]() 、
、![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() 、
、![]() 、
、![]() .
.
(1)求证:点![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(2)求![]() 的值;
的值;
(3)若![]() 、
、![]() 分别为椭圆和双曲线的右焦点,且
分别为椭圆和双曲线的右焦点,且![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由![]() ,得到
,得到![]() ,由此可证明出点
,由此可证明出点![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(2)设点![]() 、
、![]() ,求出
,求出![]() ,
,![]() ,由
,由![]() ,可得出
,可得出![]() ,从而可求出
,从而可求出![]() 的值;
的值;
(3)由![]() ,可得
,可得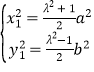 ,再由
,再由![]() ,得出
,得出![]() ,
,![]() ,由此能求出
,由此能求出![]() 的值.
的值.
(1)![]() 、
、![]() 为椭圆
为椭圆![]() 和双曲线
和双曲线![]() 的公共顶点,
的公共顶点,
![]() 、
、![]() 分别为双曲线和椭圆上不同于
分别为双曲线和椭圆上不同于![]() 、
、![]() 的动点,
的动点,
且![]() ,即
,即![]() ,即
,即![]() ,
,
因此,点![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(2)设点![]() 、
、![]() ,
,
则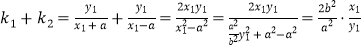 ,
,
同理可得![]() ,
,
![]() ,
,![]() ,则
,则![]() ,因此,
,因此,![]() ;
;
(3)![]() ,
,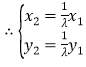 ,
,
![]() ,
,![]() ,又
,又![]() ,解得
,解得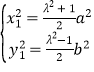 ,
,
又![]() ,
,![]() ,则
,则![]() ,则
,则![]() .
.
![]() ,
,![]() ,
,
同理可得![]() ,
,
![]() 且
且![]() ,
,![]() ,
,![]() ,
,
同理可得![]() ,
,
因此,![]() .
.

练习册系列答案
相关题目