题目内容
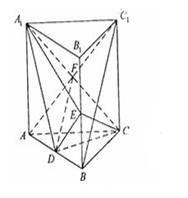
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点
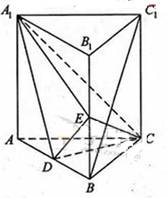
(Ⅰ)证明:BC1//平面A1CD;
(Ⅱ)设AA1=AC=CB=2,AB=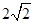 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
【答案】
(Ⅰ)详见解析;(Ⅱ)三棱锥C一A1DE的体积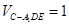 .
.
【解析】
试题分析:(Ⅰ)证明:BC1//平面A1CD,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,注意到D,分别是AB,的中点,可考虑利用三角形的中位线平行,连结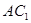 交
交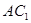 于点F,则F为
于点F,则F为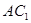 中点,连结DF,则
中点,连结DF,则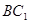 ∥DF,从而可证;(Ⅱ)求三棱锥C一A1DE的体积.求体积,关键是找高,由已知
∥DF,从而可证;(Ⅱ)求三棱锥C一A1DE的体积.求体积,关键是找高,由已知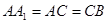 =2,
=2,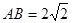 ,可知三角形
,可知三角形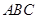 是等腰直角三角形,又因为
是等腰直角三角形,又因为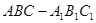 是直三棱柱,则
是直三棱柱,则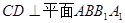 ,
,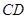 即为高,有平面几何知识可得
即为高,有平面几何知识可得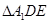 是直角三角形,可求得面积,从而可得体积.
是直角三角形,可求得面积,从而可得体积.
试题解析:(Ⅰ)连结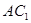 交
交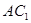 于点F,则F为
于点F,则F为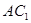 中点,又D是AB中点,连结DF,则
中点,又D是AB中点,连结DF,则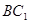 ∥DF
∥DF
因为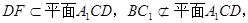 所以
所以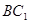 ∥平面
∥平面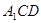
(Ⅱ)因为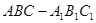 是直三棱柱,所以,
是直三棱柱,所以,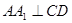 ,由已知AC=CB,D为AB的中点,所以
,由已知AC=CB,D为AB的中点,所以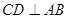 ,又
,又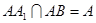 ,于是
,于是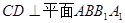 .由
.由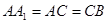 =2,
=2,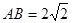 得
得
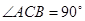 ,
,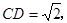
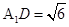 ,
,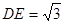 ,
,
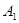 E=3,
E=3,
故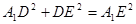 ,
,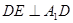 ,所以
,所以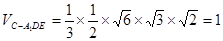 (12分)
(12分)
考点:线面平行的判定,几何体的体积.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1中,
如图,直三棱柱ABC-A1B1C1中, 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是
如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.