题目内容
已知椭圆 ,双曲线
,双曲线 和抛物线y2=2px(p>0)的离心率分别为e1、e2、e3,则( )
和抛物线y2=2px(p>0)的离心率分别为e1、e2、e3,则( )A.e1e2>e3
B.e1e2=e3
C.e1e2<e3
D.e1e2≥e3
【答案】分析:根据题意先分别表示出e1,e2和e3,然后求得e1e2的取值范围,检验选项中的结论即可.
解答:解:依题意可知e1= ,e2=
,e2= ,e3=1
,e3=1
∴e1e2= •
• =
= <1,A,B,D不正确.
<1,A,B,D不正确.
故选C.
点评:本题主要考查了圆锥曲线的共同特征,解答关键是求出e1和e2之后,根据a,b,c之间的数量关系利用不等式推导e1e2的取值范围.
解答:解:依题意可知e1=
 ,e2=
,e2= ,e3=1
,e3=1∴e1e2=
 •
• =
= <1,A,B,D不正确.
<1,A,B,D不正确.故选C.
点评:本题主要考查了圆锥曲线的共同特征,解答关键是求出e1和e2之后,根据a,b,c之间的数量关系利用不等式推导e1e2的取值范围.

练习册系列答案
相关题目
 ,双曲线
,双曲线 和抛物线
和抛物线 的离心率分别为
的离心率分别为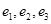 ,则( )
,则( ) B.
B. 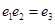 C.
C. 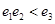 D.
D. 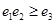
 ,双曲线
,双曲线 和抛物线y2=2px(p>0)的离心率分别为e1、e2、e3,则
和抛物线y2=2px(p>0)的离心率分别为e1、e2、e3,则 ,双曲线
,双曲线 和抛物线y2=2px(p>0)的离心率分别为e1、e2、e3,则( )
和抛物线y2=2px(p>0)的离心率分别为e1、e2、e3,则( )