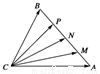
题目内容
已知△ABC中,M是BC的中点,AM=
,设内角A,B,C所对边的长分别为a,b,c,且
=
.
(1)求角A的大小;
(2)若角B=
,求△ABC的面积;
(3)求△ABC面积的最大值.
| 7 |
| cosA |
| cosC |
| ||
2b-
|
(1)求角A的大小;
(2)若角B=
| π |
| 6 |
(3)求△ABC面积的最大值.
分析:(1)利用正弦定理将边化角,再利用和角的正弦公式,即可求得结论;
(2)利用余弦定理求出AC,BC,再利用三角形的面积公式求解即可;
(3)延长AM至D,使得MD=AM,设AB=x,AC=y,利用余弦定理确定x,y之间的关系,再利用基本不等式,三角形的面积公式,即可求得结论.
(2)利用余弦定理求出AC,BC,再利用三角形的面积公式求解即可;
(3)延长AM至D,使得MD=AM,设AB=x,AC=y,利用余弦定理确定x,y之间的关系,再利用基本不等式,三角形的面积公式,即可求得结论.
解答: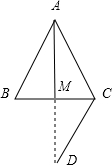 解:(1)∵
解:(1)∵
=
,
∴
=
∴2cosAsinB-
cosAsinC=
sinAcosC
∴2cosAsinB=
sin(A+C)
∴cosA=
∵0<A<π
∴A=
;
(2)设CM=x,则AC=2x,
在△AMC中,7=x2+4x2-2x•2x•cos∠ACM
∴x=1
∴AC=BC=2
∴S△ABC=
×2×2×sin120°=
;
(3)延长AM至D,使得MD=AM
设AB=x,AC=y,则28=x2+y2-2xycos150°=x2+y2+
xy≥(2+
)xy
∴xy≤
=28(2-
)
∴S△ABC=S△ACD=
xysin150°=
xy≤7(2-
)
∴x=y时,△ABC面积的最大值为7(2-
).
 解:(1)∵
解:(1)∵| cosA |
| cosC |
| ||
2b-
|
∴
| cosA |
| cosC |
| ||
2sinB-
|
∴2cosAsinB-
| 3 |
| 3 |
∴2cosAsinB=
| 3 |
∴cosA=
| ||
| 2 |
∵0<A<π
∴A=
| π |
| 6 |
(2)设CM=x,则AC=2x,
在△AMC中,7=x2+4x2-2x•2x•cos∠ACM
∴x=1
∴AC=BC=2
∴S△ABC=
| 1 |
| 2 |
| 3 |
(3)延长AM至D,使得MD=AM
设AB=x,AC=y,则28=x2+y2-2xycos150°=x2+y2+
| 3 |
| 3 |
∴xy≤
| 28 | ||
2+
|
| 3 |
∴S△ABC=S△ACD=
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
∴x=y时,△ABC面积的最大值为7(2-
| 3 |
点评:本题考查正弦定理、余弦定理的运用,考查三角形的面积公式,考查基本不等式的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
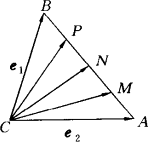
 ,
, ,试用
,试用 、
、 ,表示
,表示 、
、 、
、 .
.

 ,
, ,试用
,试用 、
、 ,表示
,表示 、
、 、
、 .
.
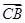 =e1,
=e1,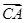 =e2,试用e1,e2表示
=e2,试用e1,e2表示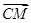 、
、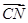 、
、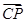 .
.